Física

ONDULATÓRIA 1 NA UECE

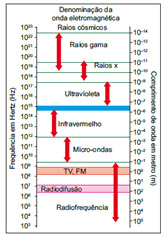
01. (UECE 85.1) Dentre as seguintes ondas eletromagnéticas, as que apresentam maior comprimento de onda são:

a) Raios gama b) Raios X c) Raios infravermelhos d) Microondas

Conforme a tabela abaixo, podemos concluir que as Microondas apresentam maior comprimento de onda.

02. (UECE 86.1) Edson verifica que um diapasão efetua 425 vibrações completas por segundo. Este diapasão entra em ressonância com uma coluna de ar de 20 cm. Neste caso, a velocidade do som no ar vale:

a) 340 m/s b) 360 m/s c) 380 m/s d) 400 m/s

V = ?.f = (4.0,2).425 = 340 m/s.

03. (UECE 86.2) Um carro de Fórmula 1, em movimento retilíneo uniforme, de velocidade V_F = 60 m/s, emite um som de frequência 560 Hz. Se o carro se desloca, passando em frente a um observador estacionário, situado à margem da pista, qual a frequência do som percebido pelo observador? Admita o ar em repouso e a velocidade do som V_S = 340 m/s.

a) 476 Hz b) 520 Hz c) 640 Hz d) 680 Hz

f? = f.(V_S + V_O)/(V_S? V_F) = 560.(340 + 0)/(340 ? 60) = 560.340/280 = 2.340 = 680 Hz.

04. (UECE 87.1) Tem-se um tubo de ambas extremidades abertas e de comprimento h. Se v for a velocidade do som no ar, a frequência fundamental que esse tubo pode produzir é:

a) v/h b) v/2h c) 2v/h d) v/4h

f_N = N.V/2.L = 1.V/2.h = V/2h.

05. (UECE 87.1) Em comparação com ondas de luz visível, as dos raios X apresentam:

a) maior velocidade.

b) menor velocidade.

c) menor comprimento de onda.

d) maior comprimento de onda.

O raio X tem frequência maior em relação a luz visível, logo apresentará um menor comprimento de onda, pois frequência e comprimento de onda são inversamente proporcionais.

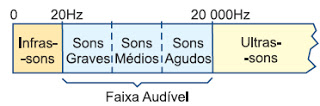
06. (UECE 87.2) Aline, completando sua maioridade, despede-se dos vestibulares de Física da UECE, com uma mensagem sonora de frequência 10 kHz. Pode-se afirmar que:

a) sua mensagem será perceptível ao ouvido humano.

b) sua mensagem não será audível, pois cai na faixa dos ultra-sons.

c) sua mensagem não será audível, pois cai na faixa dos infra-sons.

d) sua mensagem não será audível, já que é supersônica.

Um ser humano com boa audição é capaz de ouvir vibrações acústicas entre 20 Hz e 20 000 Hz aproximadamente.

07. (UECE 89.1) A luz vermelha, quando passa do vidro para o ar, tem:

a) velocidade diminuída, comprimento de onda diminuído, frequência diminuída.

b) velocidade aumentada, comprimento de onda aumentado, frequência aumentada.

c) velocidade aumentada, comprimento de onda aumentado, frequência constante.

d) velocidade constante, comprimento de onda constante, frequência aumentada.

Como o ar é o meio material de menor índice de refração, quem tem o menor índice de refração tem velocidade aumentada, comprimento de onda aumentado, frequência constante e maior ângulo de inclinação em relação à reta normal.

08. (UECE 89.2) Um observador move-se em direção a uma fonte sonora fixa que emite som de frequência f. Para que o observador perceba uma freqüência 2f, é necessário que a razão entre sua velocidade e a velocidade de propagação do som seja:

a) 1 b) 1/2 c) 2 d) 1/4

f? = f.(V_S + V_O)/(V_S? V_F) Þ 2f = f.(V_S + V_O)/(V_S+ 0) Þ 2V = V + V_O Þ V = V_O Þ V_O/V = 1.

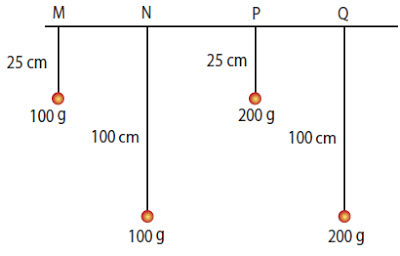
09. (UECE 90.2) Observe os quatro pêndulos da figura.

Desprezando as forças dissipativas, afirmou-se que:

I. O período de oscilação do pêndulo N é igual ao dobro do período do pêndulo M.

II. O pêndulo Q tem menor período de oscilação que o pêndulo N.

III. Os pêndulos M e P possuem mesma freqüência de oscilação.

Estão corretas:

a) somente I e III.

b) somente I e II.

c) somente II e III.

d) todas, I, II e III.

I. Como T² = 4?².L/g, temos T_M = T_P, pois o comprimento da corda é o mesmo e igual a 25 cm, assim como T_N = T_Q, pois o comprimento da corda é o mesmo e igual a 100 cm.

II. Observe que o comprimento da corda de N é 4 vezes maior do que a de M, segundo a fórmula do período nos pêndulos, temos T_N= 2.T_M.

10. (UECE 90.2) Do som mais grave ao mais agudo de uma escala musical, as ondas sonoras sofrem um aumento progressivo de:

a) amplitude b) velocidade c) freqüência d) comprimento de onda

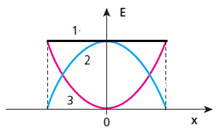
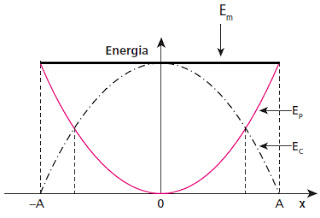
No som grave temos frequência baixa e no agudo temos frequência alta.

11. (UECE 91.1) As curvas mostradas no gráfico representam as energias potencial, cinética e mecânica (total) de uma partícula animada de movimento harmônico simples, em função da posição. A opção que identifica essas curvas é:

	ENERGIA
	Potencial	Cinética	Mecânica
a)	2	3	1
b)	1	2	3
c)	3	1	2
d)	3	2	1

Num sistema de MHS, a energia mecânica é constante, pois a força elástica é conservativa. (gráfico 1)

A energia cinética é mínima (nula) nos extremos e máxima no ponto central. (gráfico 2)

A energia potencial elástica é mínima (nula) no ponto central e máxima nos extremos. (gráfico 3)

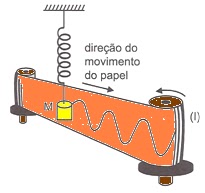
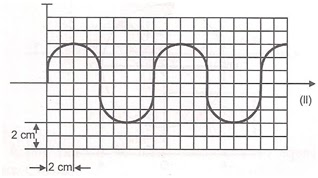
12. (UECE 91.1) Um oscilador harmônico simples consiste de uma massa M e uma mola de massa irrelevante. O sistema oscila verticalmente. Um estilete ligado a M traça uma senóide sobre uma fita de papel que avança com velocidade constante v = 4,0 cm/s, conforme indicado em (I). A figura obtida no papel está reproduzida em (II).

Com base nessas informações concluímos que o período T, a frequência f e a amplitude a do movimento são:

	T (s)	f (Hz)	a (cm)
a)	8,0	2,0	4,0
b)	2,0	0,25	6,0
c)	4,0	0,25	3,0
d)	2,0	0,50	3,0

I. A = 3 cm e ? = 4.2 = 8 cm.

II. T= ?/v = 8/4 = 2 s e f = 1/T = 1/2 = 0,5 Hz.

13. (UECE 92.1) A energia cinética de uma partícula que realiza movimento harmônico simples é máxima quando:

a) a aceleração é máxima.

b) a força é nula.

c) a elongação é máxima.

d) a força é máxima.

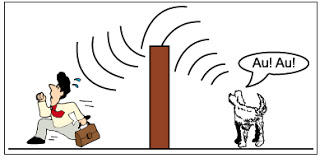
A energia cinética é máxima no ponto central (x = 0), assim: F = k.x = k.0 = 0.

14. (UECE 93.1) O menino, visto na figura, teme saltar o muro para apanhar sua bola porque está ouvindo o cão ladrar. Observa-se que as ondas sonoras contornam o muro, permitindo o menino ouvir nitidamente os latidos do cão. O fenômeno físico que explica essa situação é chamado:

a) refração b) dispersão c) difração d) polarização

A capacidade da onda em contornar os obstáculos é conhecida como a difração.

15. (UECE 93.2) Em relação ao som audível, os ultrassons, têm:

a) menor intensidade.

b) maior intensidade.

c) menor frequência.

c) maior frequência.

Se a frequência da onda mecânica é superior a 20 000 Hz, a onda se diz ultrassom e se for inferior a 20 Hz, infrassom. Dessa maneira o ultrassom apresenta uma frequência alta.

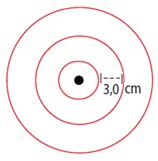
16. (UECE 93.2) Um estudante observa que, de uma torneira mal fechada, caem 30 gotas por minuto, na superfície da água de um tanque. Forma-se, então, ondas circulares cujas cristas distam 3,0 cm uma da outra, conforme ilustração ao lado. A velocidade de propagação das ondas formadas é, cm/s, igual a:

a) 1,5 b) 2,0 c) 3,0 d) 2,5

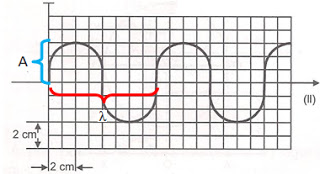
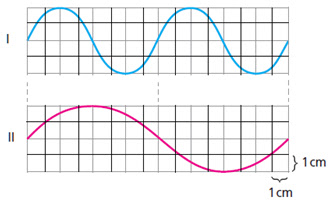
V = ?.f = 3.30/60 = 90/60 = 1,5 cm/s.

17. (UECE 95.1) As figuras representam ondas sonoras que se propagam no ar.

A afirmativa correta é:

a) o som produzido pela onda I é mais agudo do que o som produzido pela onda II.

b) o som produzido pela onda I é possui maior intensidade do que o som da onda II.

c) a frequência da onda II é maior do que da onda I.

d) as velocidades de propagação das ondas I e II, no ar, são diferentes.

Conforme as figuras ?₁ = 8 cm e ?₂ = 16 cm, logo ?₂ = 2.?₁. Como a frequência e o comprimento de onda são inversamente proporcionais, podemos concluir que f₁ = 2.f₂, sendo mais agudo a onda de maior frequência.

18. (UECE 95.1) Se I é a intensidade da onda sonora que chega ao ouvido do observador, e I₀ é a intensidade mínima que um som precisa ter para ser ouvido (limiar de audibilidade), o nível de intensidade sonora N do som percebido é dado pela expressão: N = 10.Log I/I₀. Quando I = 10.I₀, tem-se por definição, N = 1 bel. Por ser demasiado grande o bel, usa-se na prática o submúltiplo decibel (dB), assim definido: N = 10.Log I/I₀.

Situação:

Num estádio de futebol, o nível de intensidade sonora é normalmente 60 dB. No momento de um gol, a intensidade do som amplia-se 1000 vezes. Assim, o nível de intensidade sonora, no momento do gol, é em dB:

a) 120 b) 90 c) 80 d) 60

I. N =10.Log(I/I₀) = 60 dB.

II. N? = 10.Log(1000.I/I₀) = 10.Log1000 + 10.Log(I/I₀) = 30 + 60 = 90 dB.

19. (UECE 95.2) A corda sol de um violino tem 30 cm de comprimento. Quando está vibrando solta, sem ser dedilhada, a sua frequência é 196 Hz. As notas seguintes, nesta corda, são: o lá (220 Hz), o si (244 Hz), o dó (262 Hz) e o ré (294 Hz). Para fazer soar a nota si, os dedos da mão esquerda devem ser colocados a uma distância da extremidade da corda, igual aproximadamente, a:

a) 26 cm b) 24 cm c) 28 cm d) 30 cm

I. f = N.V/2.L = 1.V/2.L Þ V = f.2.L.

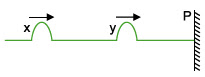
II. V₁ = V₂ Þ f.2.L = f?.2.L? Þ 196.30 = 244.L? Þ L? = 5880/244 = 24 cm.

20. (UECE 96.2) A figura mostra dois pulsos ideais, x e y, idênticos e de amplitude a, que se propaga com velocidade V em uma corda, cuja extremidade P é fixa. No instante em que ocorrer a superposição, o pulso resultante terá amplitude:

a) a b) 2 a c) a/2 d) zero

Nesse caso também há inversão de fase do pulso refletido. Por isso, como os pulsos são idênticos, quando houver a superposição do pulso refletido com o incidente a amplitude do pulso resultante será nula.

21. (UECE 97.2) A Rádio Atlântico Sul, emissora de FM, transmite ondas com freqüência de 105,7 MHz. O comprimento de onda correspondente, em metros, é aproximadamente igual a:

a) 3 b) 30 c) 300 d) 3000

? = v/f = 3.10⁸/1057.10⁵ = 3000/1057 = 3 m. (Obs.: 1 MHz = 10⁶Hz)

22. (UECE 98.2) O nível de intensidade sonora é definida por ? = 10 log 100 = 10.Log(I/I₀) 10 = Log(I/10^-12) I/10^-12= 10¹⁰ I = 10¹⁰.10^-12= 10^-2 W/m².

2) I = P/A P = I.A = 10^-2.2,5.10^-5= 2,5.10^-7 = 0,25.10^-6 = 0,25 µW. (Obs.: 2,5.10^-1 cm²= 2,5.10^-5m²)

42. (UECE 2005.1.F2) A freqüência própria de vibração da molécula d´água é 2,45 GHz. No interior de um forno de microondas, a velocidade dessas ondas é, aproximadamente, 300.000 km/s, Para aquecer alimentos por ressonância, os fornos de microondas devem produzir ondas de comprimento de onda da ordem de:

a) 1,2x10^-3 m b) 3,2x10^-4 m c) 1,2x10^-1m d) 3,2x10^-2 m

? = v/f = 3.10⁸/245.10⁷ = 30/245 = 0,12 m = 1,2.10^-1m. (Obs.: 1 GHz = 10⁹ Hz e v = 300.000 km/s = 3.10⁸ m/s)

43. (UECE 2005.1.F2) A visão humana num ambiente com pouca luz, tem um limiar de 4,0x10^-11W/m². Nessas condições, a luz penetra no olho humano com a pupila aberta com diâmetro máximo de 8 mm. A energia, em joules, que entra no olho, em 1s, é:

a) 2,0x10^-15 b) 2,0x10^-12 c) 4,0x10^-15 d) 4,0x10^-12

P = I.A = I.?.R² e E = P.?t, então:

E = I.?.(D/2)².?t = 4.10^-11.3,14.(8.10^-3/2)².1 = 4.3,14.16.10^-17 = 200,96.10^-17 = 2.10^-15 J. (Obs.: R = 8 mm = 8.10^-3 m)

44. (UECE 2006.1.F1) A figura mostra uma foto, em um dado instante, de uma onda senoidal transversal se propagando ao longo de uma corda de densidade linear 25 g/m.

Sendo 3,6 N a tensão na corda, a freqüência dessa onda, em Hertz, é:

a) 40 b) 30 c) 20 d) 10

I. V² = F/µ = 36.10^-1/25.10^-3 = 36.10²/25 V = 6.10/5 = 60/5 = 12 m/s.

II. ? = 45 ? 5 = 40 cm = 0,4 m. (distância entre duas cristas)

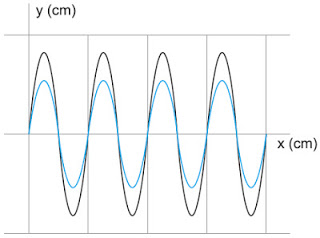
III. f = V/? =12/0,4 = 30 m/s.

45. (UECE 2006.1.F2) A figura mostra uma foto de duas ondas senoidais Ie II, de pequena amplitude, que partem simultaneamente do mesmo ponto e se propagam em um lago. Nessa situação, a interferência entre elas gera uma terceira onda.

Sobre a terceira onda produzida, podemos afirmar corretamente que:

a) a freqüência é o dobro da freqüência de I e terá a mesma velocidade de II.

b) a amplitude será igual à amplitude de II e terá o dobro da velocidade de I.

c) a amplitude será igual à diferença entre as amplitudes de I e II.

d) a amplitude será igual à soma das amplitudes de I e II e terá mesma velocidade das ondas que a originam.

A interferência não altera a velocidade de propagação das ondas e, como as ondas apresentadas no gráfico têm a mesma frequência e estão em fase, haverá interferência construtiva da qual a amplitude resultante é a soma das amplitudes das ondas originais.

46. (UECE 2006.2.F2) Um homem bate em uma das extremidades de uma haste de alumínio, de 43,5 m de comprimento. No outro extremo, seu colega, com o ouvido encostado na haste, ouve o som duas vezes (um pelo ar e outro pela haste) com intervalos de 0,12 s entre eles. Considerando que a velocidade do som no ar é 343 m/s, a velocidade do som no alumínio, em m/s, é, aproximadamente,

a) 6376 b) 3625 c) 2858 d) 343

t_AR? t_AL = 0,12 d/V_AR ? d/V_AL = 0,12 43,5/343 ? 43,5/V_AL = 0,12 43,5.V_AL ?43,5.343 = 0,12.343.V_AL 43,5.V_AL ? 41,16.V_AL = 14920,5 2,34.V_AL = 14920,5 V_AL = 14920,5/2,34 = 6376 m/s.

47. (UECE 2007.1.F2) Um sistema oscilante massa-mola possui uma energia mecânica igual a 1,0 J, uma amplitude de oscilação 0,5 m e uma velocidade máxima igual a 2 m/s. Portanto, a constante da mola, a massa e a freqüência são, respectivamente, iguais a:

a) 8,0 N/m, 1,0 kg e 4/? Hz.

b) 4,0 N/m, 0,5 kg e 4/? Hz.

c) 8,0 N/m, 0,5 kg e 2/? Hz.

d) 4,0 N/m, 1,0 kg e 2/? Hz.

I. E_CMÁX = m.V²_MÁX/2 1 = m.2²/2 m = 2/4 = 0,5 kg.

II. V_MÁX = ?.A ? = 2/0,5 = 4 rad/s.

III.? = 2?.f f = 4/2? = 2/? Hz.

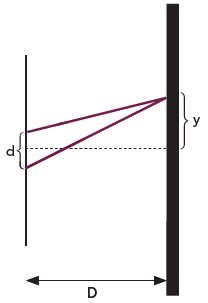
IV. ?² = k/m k = 4².0,5 = 8 N/m.

48. (UECE 2007.1.F2) Através de franjas de interferência é possível determinar características da radiação luminosa, como, por exemplo, o comprimento de onda. Considere uma figura de interferência devida a duas fendas separadas de d = 0,1 mm.

O anteparo onde as franjas são projetadas fica a D = 50 cm das fendas. Admitindo-se que as franjas são igualmente espaçadas e que a distância entre duas franjas claras consecutivas é de y = 4 mm, o comprimento de onda da luz incidente, em nm, é igual a:

a) 200 b) 400 c) 800 d) 1600

Como temos a primeira franja clara N = 0, a próxima franja N = 2.

? = 2.y.d/N.D = 2.4.10^-3.1.10^-4/2.5.10^-1 = 8.10^-7/10.10^-1= 8.10^-7/10⁰ = 8.10^-7/1 = 8.10^-7= 800.10^-9= 800 nm.

49. (UECE 2007.2.F1) Duas cordas, M e m, de um violão, estão vibrando em suas respectivas freqüências fundamentais. Sabendo-se que a freqüência maior f_M está uma oitava acima da freqüência menor f_m, e que a tensão aplicada às cordas é a mesma, a razão ?_m/?_Mentre as densidades lineares das cordas é

a) 2 b) 4 c) 8 d) 16

I. Como a freqüência f_M está uma oitava acima da freqüência f_m, temos:

i = 2ⁿ = f_M/f_m 2¹ = f_M/f_m f_M = 2.f_m.

II. Porém em cordas f = N.V/2.L, assim:

f_M = 2.f_m N.V_M/2.L = 2.N.V_m/2.L V_M = 2.V_m.

III. De acordo com a equação de Taylor V²= F/µ, temos:

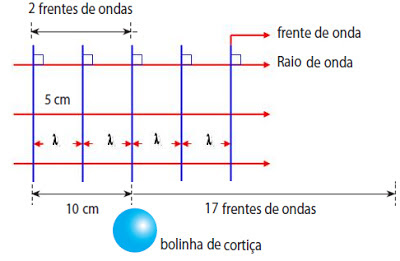
(V_M)²= (2.V_m)² F/µ_M = 4.F/µ_m ?_m/?_M= 4.

50. (UECE 2007.2.F1) Num recipiente cilíndrico de 90 cm de raio, contendo água, flutua uma bolinha de cortiça localizada a 10 cm do centro da superfície da água. Uma pequena pedra cai no centro do espelho d?água e gera ondas circulares transversais, distantes 5 cm uma da outra. O número de frentes de ondas que atingirão a bolinha de cortiça até que a primeira frente de onda atinja a borda do cilindro é:

a) 15 b) 17 c) 20 d) 22

A distância entre duas cristas consecutivas é 5 cm (? = 5 cm). Como o raio do cilindro é 90 cm, verificaremos que, nesse espaço, estarão contidos 90/5 = 18 intervalos, que são formados por 19 cristas. Veja a figura:

O número de frentes de onda que atingirão a bolinha de cortiça até que a primeira frente de onda atinja a borda do cilindro é 17.

51. (UECE 2007.2.F2) Duas ondas, A e B, de mesma amplitude e frequência, se propagam no mesmo sentido em uma região. Estas ondas se combinam e sofrem interferência totalmente construtiva, gerando uma onda resultante R. A razão entre a intensidade da onda resultante R e a intensidade de qualquer uma das ondas, A ou B, é:

a) 2 b) 3 c) 4 d) 6

1) E = k.A²/2 e I = P/4?R², assim como P = E/?t, temos:

I = k.A²/8 ?R².

2) Portanto, em uma interferência construtiva, a amplitude resultante será a soma das amplitudes: A_RES = 2A.

I_RES/I_ONDA = [k.(2A)²/8 ?R²]/(k.A²/8 ?R²) = 4.A²/A²= 4.

I. Como a energia mecânica é proporcional ao quadrado da freqüência e ao quadrado da amplitude, E = 2.?.m.f².A²no M.H.S.;

II. Podemos relacionar de forma semelhante para a intensidade média I: I = K.f².A²; em que K depende do meio e da velocidade da onda;

III. Portanto, em uma interferência construtiva, a amplitude resultante será a soma das amplitudes: A_RES= 2A.

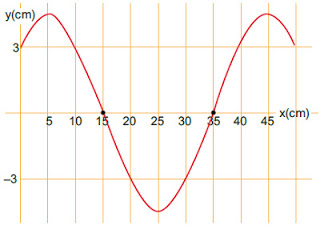
III. I_RES/I_ONDA = K.f².(2A)²/K.f².A²= 4.A²/A² = 4.

52. (UECE 2007.2.F2) Um corpo oscila com movimento harmônico simples, de acordo com a equação geral x = A cos(wt + ?). Sabendo-se que o seu período de oscilação é de uma hora e que, em t = 0, x = A, o corpo atingira o ponto igual a A/2, em:

a) 30 minutos. b) 15 minutos. c) 10 minutos. d) 6 minutos.

I. Para T = 1h = 60 min:

? = 2?/T = 2?/60 = ?/30 rad/s.

II. Sendo que em t = 0; x = A, temos:

x = A cos(wt + ?) A = A cos(?.t/30 + ?) 1 = cos(?.0/30 + ?) 1 = cos(0 + ?) 1 = cos(?) ? = 0⁰ = 0 rad.

III. Portanto, para x = A/2; o valor de t será:

x = A cos(wt + ?) A/2 = A cos(?.t/30 + ?) 1/2 = cos(?.t/30 + 0) 1/2 = cos(?.t/30) cos(?.t/30) = cos(60⁰) cos(?.t/30) = cos(?/3) ?.t/30 = ?/3 t = 30/3 = 10 min.

53. (UECE 2008.1.F1) Uma corda de 90 cm é presa por suas extremidades, em suportes fixos, como mostra a figura.

Assinale a alternativa que contém os três comprimentos de onda mais longos possíveis para as ondas estacionárias nesta corda, em centímetros.

a) 90, 60 e 30 b) 180, 90 e 60 c) 120, 90 e 60 d) 120, 60 e 30

Numa corda ? = 2L/N, assim, temos:

?₁ = 2L/1 = 2L = 2.90 = 180 cm.

?₂ = 2L/2 = L = 90 cm.

?₃= 2L/3 = 2L/3 = 2.90/3 = 180/3 = 60 cm.

54. (UECE 2008.1.F2) Quando diferentes tipos de instrumentos musicais, como flauta, saxofone e piano, produzem a mesma nota musical, os sons resultantes diferem uns dos outros devido

a) as diferentes composicões de harmônicos gerados por cada instrumento.

b) as diferentes intensidades das ondas sonoras.

c) as diferentes frequências sonoras produzidas.

d) aos diferentes comprimentos de ondas fundamentais.

O que permite distinguir os diferentes tipos de instrumentos musicais quando produzem a mesma nota musical é o timbre, que está associado às diferentes composições de harmônicos gerados por cada instrumento.

55. (UECE 2008.1.F2) Uma experiência de interferência de fenda dupla e realizada com luz azul-esverdeada de comprimento de onda igual a 512 nm. As fendas estão separadas, entre si, por uma distancia de 1,2 mm. Uma tela e localizada a uma distancia de 5,4 m do anteparo que contem as fendas. A distância, em milímetros, que separa as franjas brilhantes consecutivas vistas sobre a tela é, aproximadamente:

a) 2,3 b) 4,0 c) 5,2 d) 1,2

? = 2.y.d/N.D ?y = ?.N.D/2.d = 512.10^-9.5,4/12.10^-4= 2764,8.10^-9/12.10^-4 = 230,4.10^-5 = 2,3.10^-3m = 2,3 mm.

56. (UECE 2009.1.F2) Uma corda de piano de comprimento L, presa horizontalmente por suas extremidades, está vibrando, verticalmente, com comprimento de onda igual ao seu comprimento. No instante em que ela se mostra totalmente na horizontal, a velocidade de cada ponto ao longo da corda é

a) zero em toda extensão da corda.

b) diferente de zero em toda extensão da corda.

c) dependente da posição na corda, sempre na direção horizontal ou nula.

d) dependente da posição na corda, sempre na direção vertical ou nula.

A velocidade nos NÓS é nula e nos ventres é máxima, sendo que muda a cada harmônico, assim dependendo da sua posição na corda.

57. (UECE 2009.2.F2) Um objeto se move de modo que sua aceleração sempre é proporcional ao seu deslocamento, mas em sentido contrário, ou seja, deslocamento e aceleração têm sempre sinais opostos. Neste caso, pode-se afirmar corretamente que se trata de um movimento

a) harmônico simples.

b) uniformemente variado.

c) circular.

d) uniforme.

a = - c.x e F = m.a, logo a = F/m , onde (F = - c.m.x) c.m = k então F = - k.x (MHS), a = - ?².x.(lembrando que a_MÁX para x = - A e a_MIN para x =A).

58. (UECE 2009.2.F2) A curva que melhor representa a velocidade v(t) contra o deslocamento x(t) de um oscilador harmônico é

a) uma reta passando pela origem.

b) uma elipse centrada na origem.

c) uma senóide.

d) uma co-senóide.

V(t) = - ?.A.sen(?.t + ?) e x(t) = A.cos(?.t + ?), temos sen(?.t + ?) = - V/?.A e cos(?.t + ?) = x/A. Fazendo sen²(?.t + ?) + cos²(?.t + ?) = 1, temos V²/(?.A)²+ x²/A² = 1, lembrando uma elipse cuja equação é dada por x²/a² + y²/b² = 1 de centro (0,0).

59. (UECE 2009.2.F2) Nos itens a seguir, são dadas as equações de quatro ondas progressivas com x em metros e t em segundos:

I. y(x,t) = sen(2x ? 4t)

II. y(x,t) = 2sen(3x ? 3t)

III. y(x,t) = 5sen(2x ? 6t)

IV. y(x,t) = 10sen(4x ? t)

A onda de maior velocidade de propagação é a do item

a) II. b) IV. c) III. d) I.

y = sen (x/(1/2) ? 4.t) V₁= (1/2).4 = 2 m/s.

y = sen (x/(1/3) ? 3.t) V₂= (1/3).3 = 1 m/s.

y = sen (x/(1/2) ? 6.t) V₃ = (1/2).6 = 3 m/s.

y = sen (x/(1/4) ? 1.t) V₄ = (1/4).1 = 0,25 m/s.

60. (UECE 2010.2.F2) Os termos abaixo estão relacionados às ondas sonoras.

I - Volume se refere à intensidade da sensação auditiva produzida por um som e depende da intensidade e da frequência da onda.

II - Altura se refere a uma qualidade da onda que depende somente da sua frequência: quanto menor a frequência maior a altura.

III - Batimento se refere às flutuações na intensidade do som quando há interferência de duas ondas sonoras de mesma frequência.

IV - Timbre é uma característica que depende da frequência e da intensidade dos tons harmônicos que se superpõem para formar a onda sonora.

Está correto o que se afirma em

a) I e II, apenas.

b) II e III, apenas.

c) III e IV, apenas.

d) I e IV, apenas.

I. Verdadeiro.

II. Falso, pois a altura e frequência são inversamente proporcionais.

III. Falso, pois os batimentos sonoros são observados pela superposição entre duas ondas de freqüências próximas.

IV. Verdadeiro.

61. (UECE 2012.2.F1) Uma corda de violão de comprimento L, presa em suportes fixos nas suas extremidades, realiza oscilações harmônicas de comprimentos de onda ?. Assim, as possíveis formas de oscilação dessa corda, com n = 1, 2, 3, ..., são tais que

a) (2n+1)? = L. b) 2n? = L. c) n?/2 = L. d) n? = L.

Numa corda ? = 2.L/N, logo, L = n?/2.

- Cursos Do Blog - Termologia, Óptica E Ondas
39° aula - (última aula do 2º semestre)Cordas vibrantes / Tubos sonoros Borges e Nicolau As cordas vibrantes Ao percutirmos a corda tensa de um violão as ondas transversais produzidas refletem-se nas extremidades e superpõem-se ao longo da corda,...

- Cursos Do Blog - Termologia, Óptica E Ondas
39° aula - (última aula do 2º semestre)Cordas vibrantes / Tubos sonoros Borges e Nicolau As cordas vibrantes Ao percutirmos a corda tensa de um violão as ondas transversais produzidas refletem-se nas extremidades e superpõem-se ao longo da corda,...

- Cursos Do Blog - Termologia, Óptica E Ondas
20ª aula - 2º semestre (última)Cordas vibrantes / Tubos sonoros Borges e Nicolau As cordas vibrantes Ao percutirmos a corda tensa de um violão as ondas transversais produzidas refletem-se nas extremidades e superpõem-se ao longo da corda, formando...

- Cursos Do Blog - Termologia, Óptica E Ondas
Reflexão e Refração de Ondas Borges e Nicolau Reflexão de ondas Quando uma onda sofre reflexão, a frequência, a velocidade de propagação e o comprimento de onda não variam. Justificando: Como a frequência depende somente da fonte, concluímos...

- Resolução De Preparando-se Para As Provas 01/11
Ondas Borges e Nicolau Exercício 1 A mão da pessoa, segurando a extremidade de uma corda tensa e flexível, produz uma perturbação que se propaga ao longo da corda. A perturbação denomina-se pulso e o movimento do pulso constituí uma onda. A mão...

Física