Física
Borges e Nicolau
Equação de Gauss
Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de uma lente esférica delgada. A posição da imagem pode ser obtida por meio de uma equação: Equação de Gauss.
Objeto real: p > 0
Imagem real: p' > 0
Imagem virtual: p' < 0
Para a distância focal f, temos:
Lente convergente: f > 0
Lente divergente: f < 0
p, p? e f se relacionam pela Equação de Gauss:
1/f = 1/p + 1/p'
Aumento linear transversal A
Sejam i e o as alturas da imagem e do objeto, respectivamente. A relação entre i e o é indicada por A e recebe o nome de aumento linear transversal:
A = i/o
Convenção de sinais:
Imagem direita: A > 0
Imagem invertida: A < 0
O aumento linear transversal e as abscissas p e p? do objeto e da imagem também se relacionam:
A = -p'/p
Exercícios básicos
Exercício 1:
Um objeto linear situa-se a 30 cm de uma lente delgada convergente de distância focal 5 cm.
a) Determine a que distância da lente se forma a imagem.
b) A imagem é real ou virtual?
c) Represente a lente, o objeto e utilizando dois raios notáveis obtenha a imagem.
Exercício 2:
Um objeto linear situa-se a 12 cm de uma lente delgada divergente cuja distância focal é, em módulo, igual a 6 cm.
a) Determine a que distância do espelho se forma a imagem.
b) A imagem é real ou virtual?
c) Represente a lente, o objeto e utilizando dois raios notáveis obtenha a imagem.
Exercício 3:
A imagem real de um objeto fornecida por uma lente delgada convergente, de distância focal 30 cm, situa-se a 40 cm da lente. Determine:
a) a que distância da lente está posicionado o objeto;
b) o aumento linear transversal.
Exercício 4:
A imagem de um objeto situado diante de uma lente delgada divergente tem altura 3 vezes menor do que a do objeto. O módulo da distância focal da lente é de 15 cm. Determine a distância entre o objeto e a imagem.
Exercício 5:
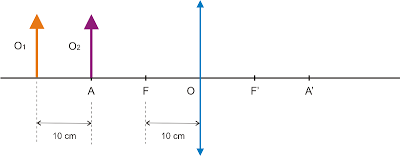
Dois objetos retilíneos de mesma altura, O1 e O2, são dispostos perpendicularmente ao eixo principal de uma lente delgada convergente, conforme indica a figura. A e A? são os pontos anti-principais objeto e imagem; F e F? os focos principais objeto e imagem. Determine:
a) a distância entre as imagens conjugadas.
b) a relação entre as alturas i1 e i2 das imagens de O1 e O2, respectivamente.
- Cursos Do Blog - Termologia, Óptica E Ondas
33ª aula Equação de Gauss. Aumento linear transversal Borges e Nicolau Equação de Gauss Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de uma lente esférica delgada. A posição da imagem pode ser...
- Cursos Do Blog - Termologia, Óptica E Ondas
33ª aula Equação de Gauss. Aumento linear transversal Borges e Nicolau Equação de Gauss Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de uma lente esférica delgada. A posição da imagem pode ser...
- Cursos Do Blog - Termologia, Óptica E Ondas
14ª aula - 2º semestre Equação de Gauss. Aumento linear transversal Borges e Nicolau Equação de Gauss Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de uma lente esférica delgada. A posição da...
- Cursos Do Blog - Termologia, Óptica E Ondas
Equação de Gauss. Aumento linear transversal Borges e Nicolau Equação de Gauss Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de um espelho esférico. A posição da imagem pode ser obtida por meio de uma...
- Cursos Do Blog - Respostas 01/11
Equação de Gauss. Aumento linear transversal Borges e Nicolau Exercício 1: Um objeto linear situa-se a 30 cm de uma lente delgada convergente de distância focal 5 cm. a) Determine a que distância da lente se forma a imagem. b) A imagem é real ou...
Física
Cursos do Blog - Termologia, Óptica e Ondas
Equação de Gauss. Aumento linear transversal
Borges e Nicolau
Equação de Gauss
Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de uma lente esférica delgada. A posição da imagem pode ser obtida por meio de uma equação: Equação de Gauss.
| Clique para ampliar |
Sejam p e p? as abscissas do objeto e da imagem em relação ao sistema de eixos cartesianos indicado na figura acima, obedecendo à seguinte convenção de sinais:
Objeto real: p > 0
Imagem real: p' > 0
Imagem virtual: p' < 0
Para a distância focal f, temos:
Lente convergente: f > 0
Lente divergente: f < 0
p, p? e f se relacionam pela Equação de Gauss:
1/f = 1/p + 1/p'
Aumento linear transversal A
Sejam i e o as alturas da imagem e do objeto, respectivamente. A relação entre i e o é indicada por A e recebe o nome de aumento linear transversal:
A = i/o
Convenção de sinais:
Imagem direita: A > 0
Imagem invertida: A < 0
O aumento linear transversal e as abscissas p e p? do objeto e da imagem também se relacionam:
A = -p'/p
Exercícios básicos
Exercício 1:
Um objeto linear situa-se a 30 cm de uma lente delgada convergente de distância focal 5 cm.
a) Determine a que distância da lente se forma a imagem.
b) A imagem é real ou virtual?
c) Represente a lente, o objeto e utilizando dois raios notáveis obtenha a imagem.
Exercício 2:
Um objeto linear situa-se a 12 cm de uma lente delgada divergente cuja distância focal é, em módulo, igual a 6 cm.
a) Determine a que distância do espelho se forma a imagem.
b) A imagem é real ou virtual?
c) Represente a lente, o objeto e utilizando dois raios notáveis obtenha a imagem.
Exercício 3:
A imagem real de um objeto fornecida por uma lente delgada convergente, de distância focal 30 cm, situa-se a 40 cm da lente. Determine:
a) a que distância da lente está posicionado o objeto;
b) o aumento linear transversal.
Exercício 4:
A imagem de um objeto situado diante de uma lente delgada divergente tem altura 3 vezes menor do que a do objeto. O módulo da distância focal da lente é de 15 cm. Determine a distância entre o objeto e a imagem.
Exercício 5:
Dois objetos retilíneos de mesma altura, O1 e O2, são dispostos perpendicularmente ao eixo principal de uma lente delgada convergente, conforme indica a figura. A e A? são os pontos anti-principais objeto e imagem; F e F? os focos principais objeto e imagem. Determine:
a) a distância entre as imagens conjugadas.
b) a relação entre as alturas i1 e i2 das imagens de O1 e O2, respectivamente.
loading...
- Cursos Do Blog - Termologia, Óptica E Ondas
33ª aula Equação de Gauss. Aumento linear transversal Borges e Nicolau Equação de Gauss Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de uma lente esférica delgada. A posição da imagem pode ser...
- Cursos Do Blog - Termologia, Óptica E Ondas
33ª aula Equação de Gauss. Aumento linear transversal Borges e Nicolau Equação de Gauss Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de uma lente esférica delgada. A posição da imagem pode ser...
- Cursos Do Blog - Termologia, Óptica E Ondas
14ª aula - 2º semestre Equação de Gauss. Aumento linear transversal Borges e Nicolau Equação de Gauss Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de uma lente esférica delgada. A posição da...
- Cursos Do Blog - Termologia, Óptica E Ondas
Equação de Gauss. Aumento linear transversal Borges e Nicolau Equação de Gauss Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de um espelho esférico. A posição da imagem pode ser obtida por meio de uma...
- Cursos Do Blog - Respostas 01/11
Equação de Gauss. Aumento linear transversal Borges e Nicolau Exercício 1: Um objeto linear situa-se a 30 cm de uma lente delgada convergente de distância focal 5 cm. a) Determine a que distância da lente se forma a imagem. b) A imagem é real ou...
