Física
9ª aula
Trabalho da força elétrica. Potencial Elétrico (II)
Borges e Nicolau
Energia potencial elétrica
Vamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como advém de uma posição dentro do campo gravitacional, recebe o nome de energia potencial gravitacional (Ep).
Em relação a um referencial no solo a energia potencial gravitacional é dada
por: Ep = m.g.h, sendo m a massa do livro, g a aceleração da gravidade e h a altura do livro em relação ao solo.
Da mesma maneira, quando você comprime ou distende uma mola, diminuindo ou aumentando seu comprimento, ela armazena energia potencial elástica (Ep), dada por Ep = K.x2/2, onde K é a constante elástica e x a deformação da mola. O referencial para o cálculo da energia potencial Ep é a mola não deformada.
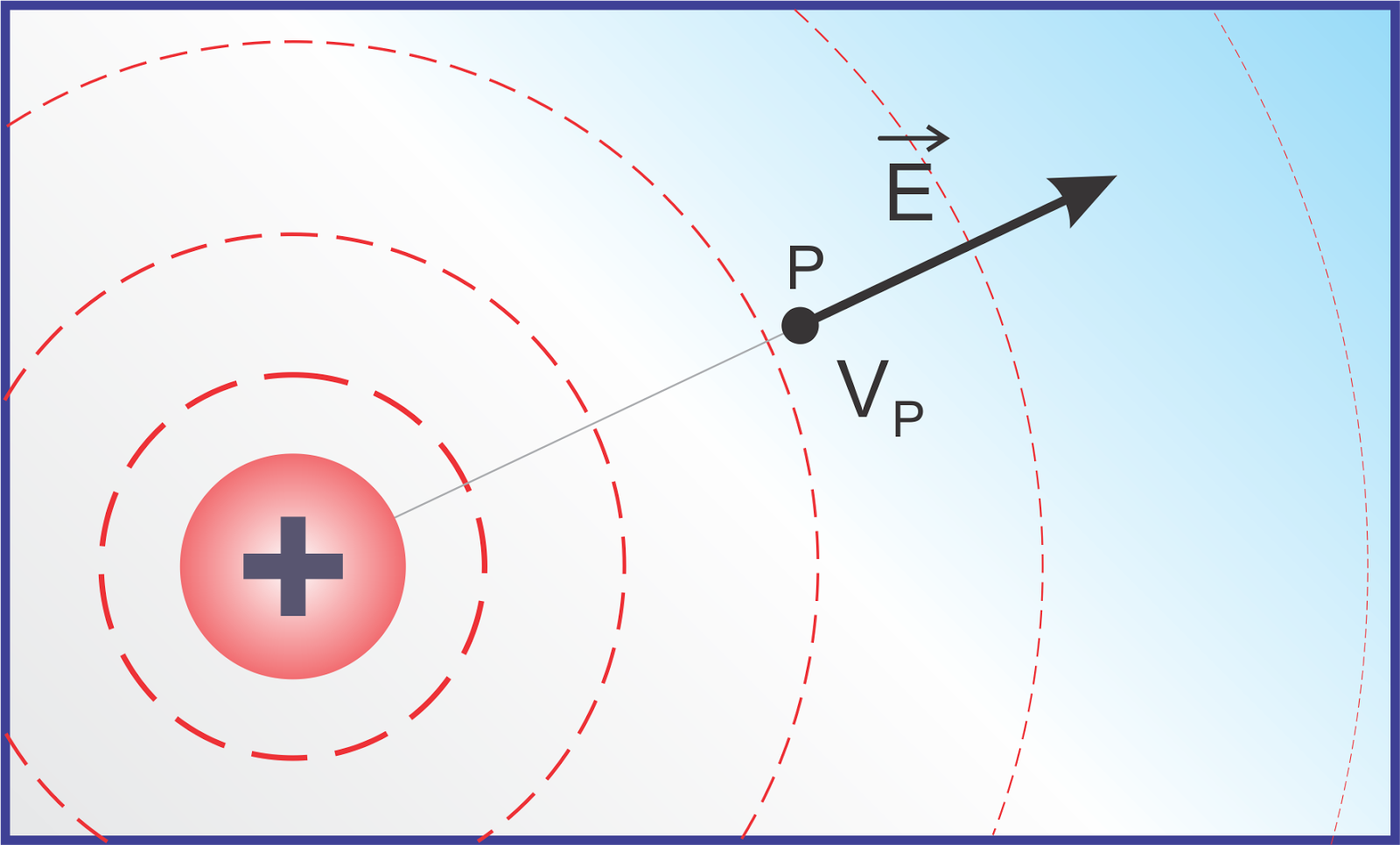
Considere, agora, o campo elétrico gerado por uma carga elétrica puntiforme Q, por exemplo positiva, fixa num ponto O. Seja P um ponto do campo. Um operador desloca uma carga elétrica puntiforme q, também positiva de um ponto bem afastado de O até o ponto P.
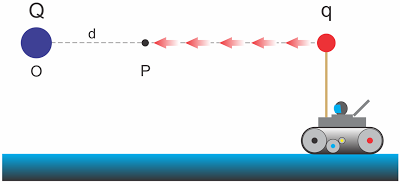
A energia despendida pelo operador (veja que Q > 0 repele q > 0) não é perdida. Fica armazenada na carga q e recebe o nome de energia potencial elétrica. A energia potencial elétrica Ep que q adquire ao ser colocada em P, situado a uma distância d de O, em relação a um referencial muito distante da carga Q (dizemos, referencial no infinito) é dada por:
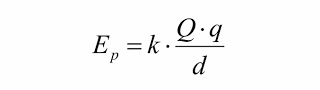
Onde k a constante eletrostática do meio. Se o meio for o vácuo a constante eletrostática é indicada por k0.
Da fórmula anterior podemos escrever
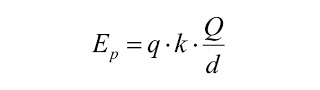
A grandeza:
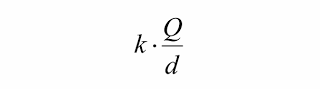
é indicada por Vp e recebe o nome de potencial elétrico no ponto P do campo da carga elétrica puntiforme Q fixa. Vamos conhecê-la melhor.
Em primeiro lugar observe que o potencial elétrico é uma grandeza escalar, que depende do meio onde a carga elétrica Q se encontra, expresso pelo valor de k. Depende do valor da carga Q que gera o campo e varia de ponto para ponto: mudando-se o valor de d, muda o valor do potencial. Assim temos:
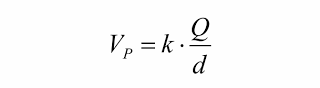
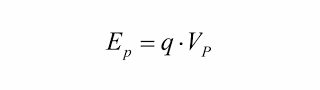
De Vp = Ep/q, concluímos que a unidade de potencial elétrico no SI é joule/coulomb (J/C) que recebe o nome de volt (V).
Potencial elétrico no campo de várias cargas elétricas puntiformes
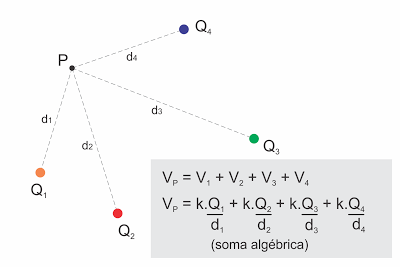
Trabalho da força elétrica no deslocamento de uma carga elétrica q do ponto A ao ponto B de um campo elétrico
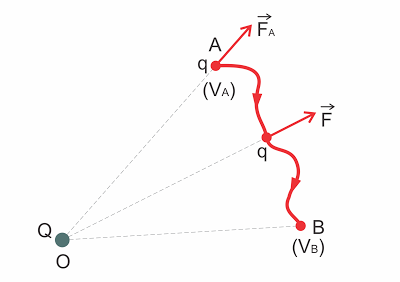
?AB = EPA - EPB = q.(VA - VB) => ?AB = q.(VA - VB)
VA - VB = U é a ddp (diferença de potencial ou tensão elétrica entre os pontos A e B).
O trabalho da força elétrica não depende da trajetória. A força elétrica é conservativa.
Exercícios básicos
Exercício 1:
Considere o campo elétrico originado por duas cargas elétricas puntiformes +2Q e ?Q, fixas nos pontos A e B, conforme indica a figura. Existem dois pontos N e M, da reta definida por A e B, nos quais o potencial elétrico resultante é nulo. Determine as distâncias de B a N e de B a M.
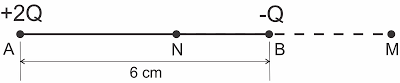
Resolução: clique aqui
Exercício 2:
Três cargas elétricas estão fixas nos vértices de um triângulo equilátero, conforme o esquema. Qual é o potencial elétrico resultante no ponto M, médio do lado AB.
Dados: Q = 10-6 C; L = 2?3 m; k0 = 9.109 N.m2/C2
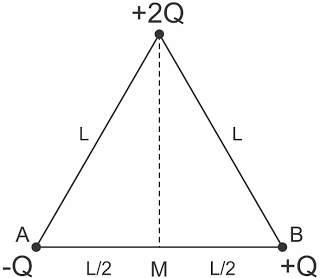
Resolução: clique aqui
Exercício 3:
No campo elétrico gerado por uma carga elétrica puntiforme Q fixa num ponto O, considere os pontos A e B. O potencial elétrico no ponto A é VA = 6.105 V. Determine:
a) O potencial elétrico do ponto B.
b) O trabalho da força elétrica que age numa partícula P eletrizada com carga elétrica q = 1 ?C, ao ser deslocada de A até B.
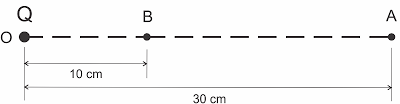
Resolução: clique aqui
Exercício 4:
Retome o exercício anterior. Com que velocidade v0 a partícula P deve ser lançada do ponto A para atingir o ponto B com velocidade nula?
A massa de P é m = 6.10-5 kg.

Resolução: clique aqui
Exercício 5:
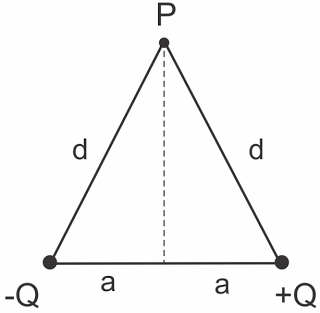
Considere o campo elétrico gerado0pela cargas elétricas puntiformes +Q e ?Q, separadas pela distância 2a e seja P um0ponto situado a uma distância d de cada carga. A constante eletrostática do meio é k0. A intensidade do vetor campo elétrico resultante e o potencial elétrico resultante0em P são, respectivamente iguais a:
a) k0.Q/d2 e k0.Q/d
b) zero e k0.Q/d
c) k0.Q/d2 e zero
d) 2.a.k0.Q/d3 e zero
e) k0.a.Q/d2 e k0.a.Q/d
Resolução: clique aqui
Exercícios de revisão
Revisão/Ex 1:
(FEI-SP)
O diagrama representa o potencial elétrico em função da distância do ponto considerado até a carga-fonte do campo.
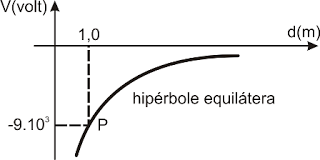
Sabe-se que o meio que envolve a carga-fonte é o vácuo. Pede-se:
a) O valor da carga-fonte Q.
b) Qual o potencial elétrico a 2 m da carga-fonte?
Dado: k0 = 9.109 N.m2/C2
Resolução: clique aqui
Revisão/Ex 2:
(Mackenzie-SP)
Duas cargas elétricas puntiformes, Q1 = 4.10-8 C e Q2 = -3.10-8 C estão localizadas em pontos A e B, separados1por uma distãncia de 10 cm, no vácuo.
a) Calcule o potencial no ponto C médio entre A e B e no ponto1D a 8 cm de a e a 6 cm de B1
b) Qual o trabalho das forças elétricas sobre1a carga q = 25.10-9 C que se desloca de C para1D?
Dado k0 = 9.109 N.m2/C2
Resolução: clique aqui
Revisão/ Ex 3:
(FUVEST)
Duas cargas -q distam a do ponto A, como indicado na figura.
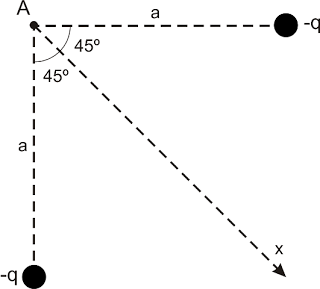
A) A que distância de A, sobre a reta Ax, devemos colocar uma carga +q para que o potencial elétrico em A seja nulo?
B) É este o único ponto do plano da figura em que a carga +q pode ser colocada para anular o potencial em A? Justifique a resposta.
Resolução: clique aqui
Revisão/ Ex 4:
(International Junior Science Olympiad)
A energia potencial eletrostática de um par de cargas elétricas puntiormes de valores Q e q, situadas a uma distância d, em relação a um referencial no ininito, é dada por
Epot = k0.Q.q/d,
em que k0 é a constante eletrostática do meio.
Considere três partículas eletrizadas com cargas elétricas iguais e fixas nos vértices de um triângulo equilátero. Se dobrássemos os valores das cargas elétricas, o que aconteceria com a energia potencial eletrostática da configuração de cargas?
a) permaneceria a mesma
b) ficaria duas vezes maior
c) ficaria quatro vezes maior
d) ficaria 8 vezes maior
e) ficaria 12 vezes maior
Resolução: clique aqui
Revisão/ Ex 5:
(UFAL)
Em cada vértice de um quadrado de lado L = ?2 m, no vácuo, está fixa uma carga puntiorme positiva, Q = 10-6 C (ver figura). Considerando que o potencial eletrostático no ininito é nulo, e dado que o valor da constante eletrostática no vácuo é 9.109 N.m2/C, assinale a alternativa com os valores do potencial eletrostático no centro do quadrado e da energia potencial eletrostática do sistema
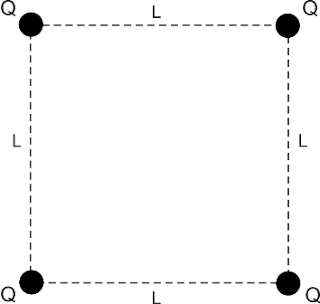
A) zero e 9.10-3.(1-2?2) J
B) 104 V e 9.10-3.(1-2?2) J
C) 3,6.104 V e 9.10-3.(1-2?2) J
D) 3,6.104 V e 9.10-3.(1+2?2) J
E) zero e 9.10-3.(1+2?2) J
Resolução: clique aqui
- Cursos Do Blog - Eletricidade
9ª aula Trabalho da força elétrica. Potencial Elétrico (II) Borges e Nicolau Energia potencial elétrica Vamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida....
- Cursos Do Blog - Eletricidade
Potencial Elétrico (II) Borges e Nicolau Energia potencial elétrica Vamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como...
- Cursos Do Blog - Eletricidade
Potencial Elétrico (I) Borges e Nicolau Energia potencial elétrica Vamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como...
- Cursos Do Blog - Eletricidade
Potencial Elétrico (II)Borges e NicolauEnergia potencial elétricaVamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como...
- Cursos Do Blog - Eletricidade
Potencial Elétrico (I)Borges e NicolauEnergia potencial elétricaVamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como...
Física
Cursos do Blog - Eletricidade

A carga positiva cria no ponto P o campo elétrico E e o potencial VP
9ª aula
Trabalho da força elétrica. Potencial Elétrico (II)
Borges e Nicolau
Energia potencial elétrica
Vamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como advém de uma posição dentro do campo gravitacional, recebe o nome de energia potencial gravitacional (Ep).
Em relação a um referencial no solo a energia potencial gravitacional é dada
por: Ep = m.g.h, sendo m a massa do livro, g a aceleração da gravidade e h a altura do livro em relação ao solo.
Da mesma maneira, quando você comprime ou distende uma mola, diminuindo ou aumentando seu comprimento, ela armazena energia potencial elástica (Ep), dada por Ep = K.x2/2, onde K é a constante elástica e x a deformação da mola. O referencial para o cálculo da energia potencial Ep é a mola não deformada.
Considere, agora, o campo elétrico gerado por uma carga elétrica puntiforme Q, por exemplo positiva, fixa num ponto O. Seja P um ponto do campo. Um operador desloca uma carga elétrica puntiforme q, também positiva de um ponto bem afastado de O até o ponto P.

A energia despendida pelo operador (veja que Q > 0 repele q > 0) não é perdida. Fica armazenada na carga q e recebe o nome de energia potencial elétrica. A energia potencial elétrica Ep que q adquire ao ser colocada em P, situado a uma distância d de O, em relação a um referencial muito distante da carga Q (dizemos, referencial no infinito) é dada por:
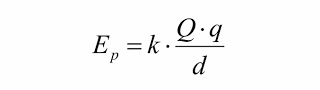
Onde k a constante eletrostática do meio. Se o meio for o vácuo a constante eletrostática é indicada por k0.
Da fórmula anterior podemos escrever
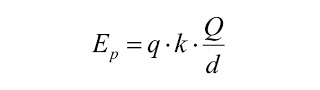
A grandeza:
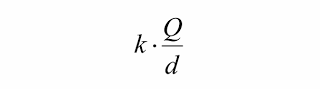
é indicada por Vp e recebe o nome de potencial elétrico no ponto P do campo da carga elétrica puntiforme Q fixa. Vamos conhecê-la melhor.
Em primeiro lugar observe que o potencial elétrico é uma grandeza escalar, que depende do meio onde a carga elétrica Q se encontra, expresso pelo valor de k. Depende do valor da carga Q que gera o campo e varia de ponto para ponto: mudando-se o valor de d, muda o valor do potencial. Assim temos:
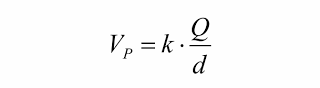
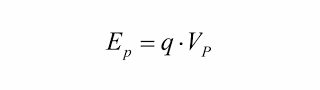
De Vp = Ep/q, concluímos que a unidade de potencial elétrico no SI é joule/coulomb (J/C) que recebe o nome de volt (V).
Potencial elétrico no campo de várias cargas elétricas puntiformes

Trabalho da força elétrica no deslocamento de uma carga elétrica q do ponto A ao ponto B de um campo elétrico

?AB = EPA - EPB = q.(VA - VB) => ?AB = q.(VA - VB)
VA - VB = U é a ddp (diferença de potencial ou tensão elétrica entre os pontos A e B).
O trabalho da força elétrica não depende da trajetória. A força elétrica é conservativa.
Exercícios básicos
Exercício 1:
Considere o campo elétrico originado por duas cargas elétricas puntiformes +2Q e ?Q, fixas nos pontos A e B, conforme indica a figura. Existem dois pontos N e M, da reta definida por A e B, nos quais o potencial elétrico resultante é nulo. Determine as distâncias de B a N e de B a M.

Resolução: clique aqui
Exercício 2:
Três cargas elétricas estão fixas nos vértices de um triângulo equilátero, conforme o esquema. Qual é o potencial elétrico resultante no ponto M, médio do lado AB.
Dados: Q = 10-6 C; L = 2?3 m; k0 = 9.109 N.m2/C2

Resolução: clique aqui
Exercício 3:
No campo elétrico gerado por uma carga elétrica puntiforme Q fixa num ponto O, considere os pontos A e B. O potencial elétrico no ponto A é VA = 6.105 V. Determine:
a) O potencial elétrico do ponto B.
b) O trabalho da força elétrica que age numa partícula P eletrizada com carga elétrica q = 1 ?C, ao ser deslocada de A até B.

Resolução: clique aqui
Exercício 4:
Retome o exercício anterior. Com que velocidade v0 a partícula P deve ser lançada do ponto A para atingir o ponto B com velocidade nula?
A massa de P é m = 6.10-5 kg.

Resolução: clique aqui
Exercício 5:
Considere o campo elétrico gerado0pela cargas elétricas puntiformes +Q e ?Q, separadas pela distância 2a e seja P um0ponto situado a uma distância d de cada carga. A constante eletrostática do meio é k0. A intensidade do vetor campo elétrico resultante e o potencial elétrico resultante0em P são, respectivamente iguais a:
a) k0.Q/d2 e k0.Q/d
b) zero e k0.Q/d
c) k0.Q/d2 e zero
d) 2.a.k0.Q/d3 e zero
e) k0.a.Q/d2 e k0.a.Q/d

Resolução: clique aqui
Exercícios de revisão
Revisão/Ex 1:
(FEI-SP)
O diagrama representa o potencial elétrico em função da distância do ponto considerado até a carga-fonte do campo.

Sabe-se que o meio que envolve a carga-fonte é o vácuo. Pede-se:
a) O valor da carga-fonte Q.
b) Qual o potencial elétrico a 2 m da carga-fonte?
Dado: k0 = 9.109 N.m2/C2
Resolução: clique aqui
Revisão/Ex 2:
(Mackenzie-SP)
Duas cargas elétricas puntiformes, Q1 = 4.10-8 C e Q2 = -3.10-8 C estão localizadas em pontos A e B, separados1por uma distãncia de 10 cm, no vácuo.
a) Calcule o potencial no ponto C médio entre A e B e no ponto1D a 8 cm de a e a 6 cm de B1
b) Qual o trabalho das forças elétricas sobre1a carga q = 25.10-9 C que se desloca de C para1D?
Dado k0 = 9.109 N.m2/C2
Resolução: clique aqui
Revisão/ Ex 3:
(FUVEST)
Duas cargas -q distam a do ponto A, como indicado na figura.

A) A que distância de A, sobre a reta Ax, devemos colocar uma carga +q para que o potencial elétrico em A seja nulo?
B) É este o único ponto do plano da figura em que a carga +q pode ser colocada para anular o potencial em A? Justifique a resposta.
Resolução: clique aqui
Revisão/ Ex 4:
(International Junior Science Olympiad)
A energia potencial eletrostática de um par de cargas elétricas puntiormes de valores Q e q, situadas a uma distância d, em relação a um referencial no ininito, é dada por
Epot = k0.Q.q/d,
em que k0 é a constante eletrostática do meio.
Considere três partículas eletrizadas com cargas elétricas iguais e fixas nos vértices de um triângulo equilátero. Se dobrássemos os valores das cargas elétricas, o que aconteceria com a energia potencial eletrostática da configuração de cargas?
a) permaneceria a mesma
b) ficaria duas vezes maior
c) ficaria quatro vezes maior
d) ficaria 8 vezes maior
e) ficaria 12 vezes maior
Resolução: clique aqui
Revisão/ Ex 5:
(UFAL)
Em cada vértice de um quadrado de lado L = ?2 m, no vácuo, está fixa uma carga puntiorme positiva, Q = 10-6 C (ver figura). Considerando que o potencial eletrostático no ininito é nulo, e dado que o valor da constante eletrostática no vácuo é 9.109 N.m2/C, assinale a alternativa com os valores do potencial eletrostático no centro do quadrado e da energia potencial eletrostática do sistema

A) zero e 9.10-3.(1-2?2) J
B) 104 V e 9.10-3.(1-2?2) J
C) 3,6.104 V e 9.10-3.(1-2?2) J
D) 3,6.104 V e 9.10-3.(1+2?2) J
E) zero e 9.10-3.(1+2?2) J
Resolução: clique aqui
loading...
- Cursos Do Blog - Eletricidade
9ª aula Trabalho da força elétrica. Potencial Elétrico (II) Borges e Nicolau Energia potencial elétrica Vamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida....
- Cursos Do Blog - Eletricidade
Potencial Elétrico (II) Borges e Nicolau Energia potencial elétrica Vamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como...
- Cursos Do Blog - Eletricidade
Potencial Elétrico (I) Borges e Nicolau Energia potencial elétrica Vamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como...
- Cursos Do Blog - Eletricidade
Potencial Elétrico (II)Borges e NicolauEnergia potencial elétricaVamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como...
- Cursos Do Blog - Eletricidade
Potencial Elétrico (I)Borges e NicolauEnergia potencial elétricaVamos inicialmente fazer algumas analogias. Quando você ergue um livro para colocá-lo numa estante, a energia que você despende não é perdida. Ela fica armazenada no livro e, como...
