Física

Professor Carlos Magno Torres
- Leituras Do Blog
Crivo de Eratóstenes Borges e Nicolau Uma contribuição importante do matemático e filósofo gergo Eratóstenes (276 aC - 194 aC), foi o método usado para a determinação de todos o números primos, até um certo limite desejado, conhecido como Crivo...
- Leituras Do Blog
Mas, ...onde aparece o número ?e??Continuação de "e, o número da natureza!" (aqui) Professor Carlos Magno TorresPor que o número e é considerado o ?Número da Natureza?? Por que os logaritmos de base e são chamados de ?Logaritmos Naturais??...
- Leituras Do Blog
O Fantástico e Onipresente Número PI (?) Professor Carlos Magno Torres Pelo fato de o número pi ser representado por uma letra do alfabeto grego, poderíamos pensar que os antigos gregos tenham sido os primeiros a utilizá-lo....
- Leituras Do Blog
Cadê minhas moléculas!? Professor Carlos Magno Torres Vamos supor que, de algum modo muito especial, fosse possível ?pintar? as moléculas de água contidas em um copo de 180 ml. A seguir, jogaríamos o conteúdo desse copo no mar e, de algum outro...
- Números
Sistema decimal e sistema binário Nicolau Gilberto Ferraro Normalmente utilizamos, ao escrever um número qualquer, o sistema decimal, isto é, o número é escrito como potências de 10. Por exemplo, o número 749 é igual a 7.102 + 4.101 + 9.100,...
Física
Leituras do Blog

e, o número da natureza!
Professor Carlos Magno Torres
Em uma leitura anterior conhecemos algumas propriedades e particularidades muito interessantes do incrível número PI (?). Nesta leitura vamos conhecer outro magnífico número, conhecido como número de Napier (John Napier, 1550 ? 1617), embora o símbolo que representa esse número, a letra e, tenha sido usado primeiramente por Euler1 (Leonhard Euler, 1707 ? 1783). Contrariamente ao PI, que conhecemos logo nos nossos primeiros anos de escola, o e só aparece na nossa vida escolar mais ou menos no final da segunda série ou na terceira série do ensino médio. Muitos estudantes nem tem a oportunidade de conhecê-lo.
Na figura do título desta leitura apresentamos o número e com suas cinquenta primeiras casas decimais.
Assim como o PI, o número ?e? é irracional, isto é, não pode ser escrito como razão entre dois inteiros, e também é transcendental, isto é, ele não pode ser obtido como raiz de uma equação algébrica polinomial2.
Mas então,... como obter o e? Para que serve esse número? Onde ele aparece?
Bem, temos alguns caminhos para chegar a ele e várias são as situações nas quais ele está presente. Acompanhe.
1Euler pronuncia-se "óiler". "Freud" explica.
2Evidentemente ? é raiz da equação x ? ? = 0. Mas essa equação não é algébrica, isto é, seus coeficientes não são inteiros e, além disso, ela não nos dá o valor de ?!
2Evidentemente ? é raiz da equação x ? ? = 0. Mas essa equação não é algébrica, isto é, seus coeficientes não são inteiros e, além disso, ela não nos dá o valor de ?!
Expressões que levam ao "e"
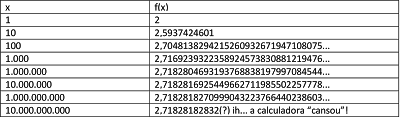
1. Euler demostrou que a função f(x) = (1 + 1/x)x converge para o número e quando x cresce indefinidamente. A tabela abaixo mostra valores de f(x) para valores significativos de x.
x
x

Clique para ampliar
Como se vê, os valores de f(x) são cada vez maiores, mas tendem a um limite.
2. Podemos obter o número e, com a precisão que desejarmos, adicionando mais e mais parcelas à série infinita a seguir, descoberta por Isaac Newton em 1665:
e = 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + ... + 1/n!
O símbolo "n!" lê-se "n fatorial". Na tabela abaixo mostram-se os fatoriais de alguns números naturais a partir do zero.
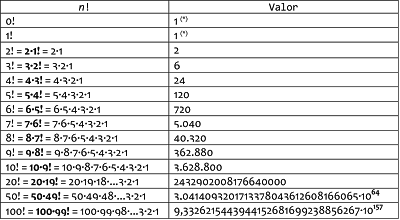
(*)Evidentemente, os fatoriais de zero e um não podem ser calculados por produtos de fatores, como são calculados os fatoriais de 2 em diante.3
Assim, a somatória acima fica:
e = 1/1+1/1+1/2+1/6+1/24+1/120+1/720+1/5040+...+1/n!
Se somarmos até a oitava parcela já teremos e ? 2,718254, com precisão até décimos de milésimos!
Há uma maneira fácil de se obter a soma dessa série, para quantas parcelas quisermos. Veja:
divide por 1: xxxxxx1xxxxxxxxxxxxxxxxxxsoma (e ?)
divide por 2: xxxxxx1xxxxxxxxxxxxxxxxxxx2
divide por 3: xxxxxx0,5xxxxxxxxxxxxxxxxxx2,5
divide por 4: xxxxxx0,1666...xxxxxxxxxxx2,666...
divide por 5: xxxxxx0,041666...xxxxxxxxx2,708333...
divide por 6: xxxxxx0,008333...xxxxxxxxx2,71666...
divide por 7: xxxxxx0,0013888...xxxxxxxx2,7180555...
divide por 8: xxxxxx0,00019841...xxxxxxx2,71825397...
...xxxxxxxx... xxxxxx0,00002480...xxxxxxx2,71827877...
xxxxx? xxxxxxxxxxxxxxxxx?xxxxxxxxxxxxxxxxxxx ?
Essa soma ?converge? mais rapidamente para o valor de e que a função f(x) acima. Portanto vale a igualdade demonstrada por Euler:
[(1 + 1/x)x]x?? = 1/0!+1/1!+1/2!+1/3!+1/4!+1/5!+...+1/n! = e
3. Aproximações excelentes para o e:
? e ? (?4 + ?5)1/6 ? 2,71828180862... (precisão até décimo de milionésimo!)
? e ? 271801/99990 ? 2,71828182818... (precisão até bilionésimo!)
Acho que já está bom, não?!
3Existe uma função, denominada função Gama de Euler, que calcula o fatorial de qualquer número real, exceto para os inteiros negativos, para os quais não se define fatorial. Calculadoras eletrônicas científicas mais avançadas tem essa função residente.
Mas, ...onde aparece o número ?e?? Na próxima sexta-feira você saberá...
2. Podemos obter o número e, com a precisão que desejarmos, adicionando mais e mais parcelas à série infinita a seguir, descoberta por Isaac Newton em 1665:
e = 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + ... + 1/n!
O símbolo "n!" lê-se "n fatorial". Na tabela abaixo mostram-se os fatoriais de alguns números naturais a partir do zero.

Clique para ampliar
(*)Evidentemente, os fatoriais de zero e um não podem ser calculados por produtos de fatores, como são calculados os fatoriais de 2 em diante.3
Assim, a somatória acima fica:
e = 1/1+1/1+1/2+1/6+1/24+1/120+1/720+1/5040+...+1/n!
Se somarmos até a oitava parcela já teremos e ? 2,718254, com precisão até décimos de milésimos!
Há uma maneira fácil de se obter a soma dessa série, para quantas parcelas quisermos. Veja:
divide por 1: xxxxxx1xxxxxxxxxxxxxxxxxxsoma (e ?)
divide por 2: xxxxxx1xxxxxxxxxxxxxxxxxxx2
divide por 3: xxxxxx0,5xxxxxxxxxxxxxxxxxx2,5
divide por 4: xxxxxx0,1666...xxxxxxxxxxx2,666...
divide por 5: xxxxxx0,041666...xxxxxxxxx2,708333...
divide por 6: xxxxxx0,008333...xxxxxxxxx2,71666...
divide por 7: xxxxxx0,0013888...xxxxxxxx2,7180555...
divide por 8: xxxxxx0,00019841...xxxxxxx2,71825397...
...xxxxxxxx... xxxxxx0,00002480...xxxxxxx2,71827877...
xxxxx? xxxxxxxxxxxxxxxxx?xxxxxxxxxxxxxxxxxxx ?
Essa soma ?converge? mais rapidamente para o valor de e que a função f(x) acima. Portanto vale a igualdade demonstrada por Euler:
[(1 + 1/x)x]x?? = 1/0!+1/1!+1/2!+1/3!+1/4!+1/5!+...+1/n! = e
3. Aproximações excelentes para o e:
? e ? (?4 + ?5)1/6 ? 2,71828180862... (precisão até décimo de milionésimo!)
? e ? 271801/99990 ? 2,71828182818... (precisão até bilionésimo!)
Acho que já está bom, não?!
3Existe uma função, denominada função Gama de Euler, que calcula o fatorial de qualquer número real, exceto para os inteiros negativos, para os quais não se define fatorial. Calculadoras eletrônicas científicas mais avançadas tem essa função residente.
Mas, ...onde aparece o número ?e?? Na próxima sexta-feira você saberá...
loading...
- Leituras Do Blog
Crivo de Eratóstenes Borges e Nicolau Uma contribuição importante do matemático e filósofo gergo Eratóstenes (276 aC - 194 aC), foi o método usado para a determinação de todos o números primos, até um certo limite desejado, conhecido como Crivo...
- Leituras Do Blog
Mas, ...onde aparece o número ?e??Continuação de "e, o número da natureza!" (aqui) Professor Carlos Magno TorresPor que o número e é considerado o ?Número da Natureza?? Por que os logaritmos de base e são chamados de ?Logaritmos Naturais??...
- Leituras Do Blog
O Fantástico e Onipresente Número PI (?) Professor Carlos Magno Torres Pelo fato de o número pi ser representado por uma letra do alfabeto grego, poderíamos pensar que os antigos gregos tenham sido os primeiros a utilizá-lo....
- Leituras Do Blog
Cadê minhas moléculas!? Professor Carlos Magno Torres Vamos supor que, de algum modo muito especial, fosse possível ?pintar? as moléculas de água contidas em um copo de 180 ml. A seguir, jogaríamos o conteúdo desse copo no mar e, de algum outro...
- Números
Sistema decimal e sistema binário Nicolau Gilberto Ferraro Normalmente utilizamos, ao escrever um número qualquer, o sistema decimal, isto é, o número é escrito como potências de 10. Por exemplo, o número 749 é igual a 7.102 + 4.101 + 9.100,...
