Física
Como se explica?
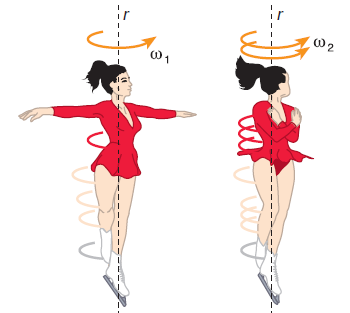
Uma bailarina gira em torno de seu eixo vertical1de rotação r com os braços estendidos e com velocidade angular ?1. Fechando os braços sua velocidade angular passa a ser ?2 maior do que ?1, isto é, a bailarina passa a girar com velocidade angular maior. Como se explica este fato?
A explicação está na conservação do momento angular. Vamos estudar este assunto. Acompanhe a teoria.
Momento angular ou momento da quantidade de movimento m.v de um ponto material P, em relação a um ponto O, é a grandeza vetorial L que possui as seguintes características:
Módulo: L = mvd, onde d é a distância do ponto O à reta s, suporte da velocidade v do ponto material.
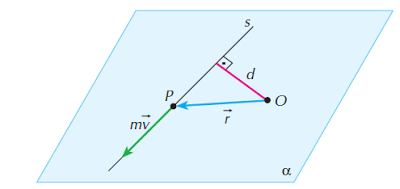
Direção: da reta perpendicular ao plano ? definido pela reta s e pelo ponto O.
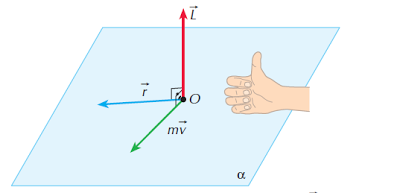
Sentido: dado pela regra da mão direita, conforme indica a figura abaixo
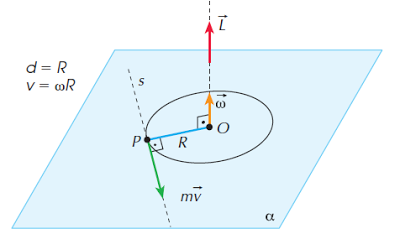
Considere um ponto material P que realiza um movimento circular uniforme de centro O, com velocidade de módulo v e velocidade angular ?.
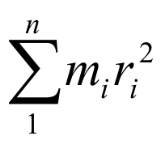
é o momento de inércia do corpo em relação ao eixo de rotação. Logo:
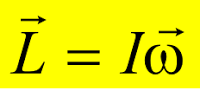
O momento de inércia I depende da massa do corpo e de como ela se distribui em relação ao eixo de rotação. O momento de inércia mede a resistência que o corpo opõe à rotação. De fato, de L = I.?, concluímos que para o mesmo L, quanto maior for I menor é o ?.
Se o momento (torque) das forças que atuam num corpo em rotação é nulo, então o momento angular permanece constante.
Nestas condições, resulta em módulo:
Se o corpo for deformável, sendo L = I.? constante, vem que se I aumenta ? diminui e se I diminui, ? aumenta.
É o caso da bailarina. Fechando os braços, o momento de inércia diminui de para I1 para I2 (I2 < I1) e sua velocidade angular varia de ?1 para ?2.
Como I1?1 = I2?2, resulta ?2 > ?1.
(Fonte: www.moderna.com.br/fundamentos)
Clique em Temas especiais
- Cursos Do Blog - Mecânica
Equilíbrio Estático de um corpo extenso Borges e Nicolau Uma barra homogênea de comprimento 4 m e de peso P = 12 N está apoiada nos pontos A e B, conforme a figura. Vamos determinar as intensidades das forças FA e FB que os apoios exercem na barra....
- Cursos Do Blog - Mecânica
Movimentos Circulares (I) Borges e Nicolau Movimento circular uniforme (MCU) É um movimento que se realiza com velocidade escalar v constante e cuja trajetória é uma circunferência ou um arco de circunferência. No MCU a velocidade2vetorial tem módulo...
- Cursos Do Blog - Mecânica
Equilíbrio Estático de um corpo extenso Borges e Nicolau Uma barra homogênea de comprimento 4 m e de peso P = 12 N está apoiada nos pontos A e B, conforme a figura. Vamos determinar as intensidades das forças FA e FB que os apoios exercem na barra....
- Preparando-se Para As Provas
Movimento Circular Uniforme (MCU) (II) Borges e Nicolau TRANSMISSÃO DE MOVIMENTO CIRCULAR UNIFORME Clique para ampliar Exercícios básicos Exercício 1Duas polias, 1 e 2, são ligadas por uma correia. A polia 1 possui raio R1 , gira com velocidade...
- Momento, Definição
Clique para ampliar Como se calcula o momento de uma força em relação a um ponto? Borges e Nicolau Para o cálculo do momento MO de uma força F em relação a um ponto O devemos levar em conta a intensidade F da força e a distância d do ponto...
Física
Leituras do Blog
Como se explica?
Uma bailarina gira em torno de seu eixo vertical1de rotação r com os braços estendidos e com velocidade angular ?1. Fechando os braços sua velocidade angular passa a ser ?2 maior do que ?1, isto é, a bailarina passa a girar com velocidade angular maior. Como se explica este fato?

A explicação está na conservação do momento angular. Vamos estudar este assunto. Acompanhe a teoria.
Momento angular ou momento da quantidade de movimento de um ponto material.
Momento angular ou momento da quantidade de movimento m.v de um ponto material P, em relação a um ponto O, é a grandeza vetorial L que possui as seguintes características:
Módulo: L = mvd, onde d é a distância do ponto O à reta s, suporte da velocidade v do ponto material.

Direção: da reta perpendicular ao plano ? definido pela reta s e pelo ponto O.
Sentido: dado pela regra da mão direita, conforme indica a figura abaixo

O dedo polegar indica o sentido de L, enquanto os demais dedos são semidobrados no sentido de r para mv.
Momento angular de um ponto P que realiza movimento circular uniforme
Considere um ponto material P que realiza um movimento circular uniforme de centro O, com velocidade de módulo v e velocidade angular ?.

Vamos calcular o módulo do momento angular L, em relação ao centro O:
De L = mvd e sendo d = R e v = ?R, vem:
L = m.?.R.R => L = m.R2.?
Vetorialmente, sendo ? a velocidade de rotação cujo sentido é o mesmo de L e cujo módulo é igual à velocidade angular ?, temos:
L = m.R2.?
A grandeza escalar m.R2 é indicada pela letra I e recebe o nome de momento de inércia do ponto material P em relação ao ponto O.
Assim, temos:
L = I.?
No SI a unidade de momento de inércia é kg.m2
Considere um corpo em rotaçãoi uniforme, em torno de um eixo fixo.
Para cada ponto Pi, de massa mi e a uma distância ri do eixo de rotação, podemos escrever: Li = miri2?, onde ? é o vetor de rotação, suposto constante.
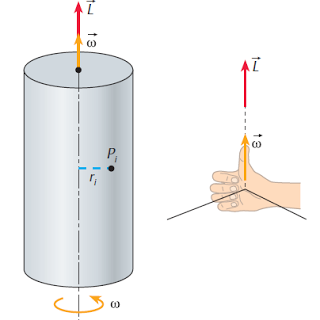
O momento angular total L do corpo é dado por:
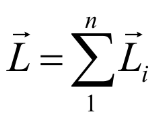
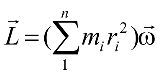 Mas:
Mas:
Vetorialmente, sendo ? a velocidade de rotação cujo sentido é o mesmo de L e cujo módulo é igual à velocidade angular ?, temos:
L = m.R2.?
A grandeza escalar m.R2 é indicada pela letra I e recebe o nome de momento de inércia do ponto material P em relação ao ponto O.
Assim, temos:
L = I.?
No SI a unidade de momento de inércia é kg.m2
Momento angular de um corpo extenso em rotação uniforme em torno de um eixo fixo
Considere um corpo em rotaçãoi uniforme, em torno de um eixo fixo.
Para cada ponto Pi, de massa mi e a uma distância ri do eixo de rotação, podemos escrever: Li = miri2?, onde ? é o vetor de rotação, suposto constante.

O momento angular total L do corpo é dado por:
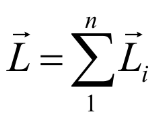
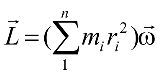
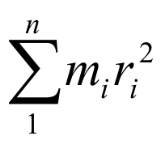
é o momento de inércia do corpo em relação ao eixo de rotação. Logo:
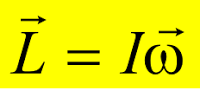
O momento de inércia I depende da massa do corpo e de como ela se distribui em relação ao eixo de rotação. O momento de inércia mede a resistência que o corpo opõe à rotação. De fato, de L = I.?, concluímos que para o mesmo L, quanto maior for I menor é o ?.
Conservação do momento angular
Se o momento (torque) das forças que atuam num corpo em rotação é nulo, então o momento angular permanece constante.
Nestas condições, resulta em módulo:
L = I? = constante
xSe o corpo for deformável, sendo L = I.? constante, vem que se I aumenta ? diminui e se I diminui, ? aumenta.
É o caso da bailarina. Fechando os braços, o momento de inércia diminui de para I1 para I2 (I2 < I1) e sua velocidade angular varia de ?1 para ?2.
Como I1?1 = I2?2, resulta ?2 > ?1.
(Fonte: www.moderna.com.br/fundamentos)
Clique em Temas especiais
loading...
- Cursos Do Blog - Mecânica
Equilíbrio Estático de um corpo extenso Borges e Nicolau Uma barra homogênea de comprimento 4 m e de peso P = 12 N está apoiada nos pontos A e B, conforme a figura. Vamos determinar as intensidades das forças FA e FB que os apoios exercem na barra....
- Cursos Do Blog - Mecânica
Movimentos Circulares (I) Borges e Nicolau Movimento circular uniforme (MCU) É um movimento que se realiza com velocidade escalar v constante e cuja trajetória é uma circunferência ou um arco de circunferência. No MCU a velocidade2vetorial tem módulo...
- Cursos Do Blog - Mecânica
Equilíbrio Estático de um corpo extenso Borges e Nicolau Uma barra homogênea de comprimento 4 m e de peso P = 12 N está apoiada nos pontos A e B, conforme a figura. Vamos determinar as intensidades das forças FA e FB que os apoios exercem na barra....
- Preparando-se Para As Provas
Movimento Circular Uniforme (MCU) (II) Borges e Nicolau TRANSMISSÃO DE MOVIMENTO CIRCULAR UNIFORME Clique para ampliar Exercícios básicos Exercício 1Duas polias, 1 e 2, são ligadas por uma correia. A polia 1 possui raio R1 , gira com velocidade...
- Momento, Definição
Clique para ampliar Como se calcula o momento de uma força em relação a um ponto? Borges e Nicolau Para o cálculo do momento MO de uma força F em relação a um ponto O devemos levar em conta a intensidade F da força e a distância d do ponto...
