Física
- Leituras Do Blog
Crivo de Eratóstenes Borges e Nicolau Uma contribuição importante do matemático e filósofo gergo Eratóstenes (276 aC - 194 aC), foi o método usado para a determinação de todos o números primos, até um certo limite desejado, conhecido como Crivo...
- Leituras Do Blog
e, o número da natureza! Professor Carlos Magno Torres Em uma leitura anterior conhecemos algumas propriedades e particularidades muito interessantes do incrível número PI (?). Nesta leitura vamos conhecer outro magnífico número, conhecido...
- Leituras Do Blog
O Fantástico e Onipresente Número PI (?) Professor Carlos Magno Torres Pelo fato de o número pi ser representado por uma letra do alfabeto grego, poderíamos pensar que os antigos gregos tenham sido os primeiros a utilizá-lo....
- Leituras Do Blog
Eratóstenes Borges e Nicolau Eratóstenes, matemático e filósofo grego nasceu em 276 aC em Cirene, cidade da qual só restam ruinas, na atual Líbia, e morreu em 194 aC, na cidade de Alexandria. Foi diretor da Biblioteca de Alexandria, sendo...
- A Aceleração De Um Ponto Material é Definida Por A= -k/x. Determinou-se Exeperimentalmente Que V= 3m/s Quando X = 500mm. Obter A Velocidade Quando X = 750 Mm E A Posição Do Ponto Para A Qual Sua Velocidade é Nula.
Anônimo disse... no MUV, a aceleração é constante e x = at²/2, desse modo: x = at²/2 x = -kt² / 2x x² = -kt²/2 x = t.raiz.quadrada(-k/2), (com k =< 0) , lembrando que v = dx/dt, temos v = raiz.quadrada(-k/2) , para x = 500 mm, v = 3, então:...
Física
Leituras do Blog
Algoritmo iterativo para se obter a raiz quadrada de um número real positivo
Um pouco de "matemática antiga", também usada por Newton
Um pouco de "matemática antiga", também usada por Newton
Professor Carlos Magno Torres
Inicialmente vamos "traduzir" os termos "algoritmo" e "iterativo". Algoritmo é um conjunto de procedimentos que levam à obtenção de um resultado. O processo de divisão, que aprendemos no início da nossa vida escolar, é um algoritmo. O conhecido método de Bh?skara, utilizado na resolução de equações do segundo grau, também é um algoritmo.
No dicionário, iterar significa repetir. Um Processo Iterativo é a aplicação repetida de um mesmo algoritmo, até obter- se um resultado com a precisão desejada.
O algoritmo que vamos mostrar a seguir é um método simples de chegarmos à raiz quadrada de um número N, com excelente precisão, em três ou quatro iterações. Esse método já era usado na antiga Babilônia (2000 a.C.) e, posteriormente por Heron em Alexandria (10 d.C ? 70 d.C.).
Obviamente, é muito mais fácil pressionarmos as teclas "2" e "?" de uma calculadora para obtermos a raiz quadrada de dois. Mas,... e se a nossa calculadora não tiver a tecla "?", como podemos nos arranjar...? O algoritmo que vamos descrever era usado num tempo em que a ciência estava sendo escrita à luz de velas, em lápides de argila ou em folhas de papiro. É uma verdadeira "jóia" produzida pela inteligência humana!
Esse algoritmo é empregado ainda hoje (!) pelas calculadoras eletrônicas dotadas da tecla "?". Elas fazem os mesmos procedimentos que vamos fazer, só que num tempo muuuito menor.
Acompanhe. É interessante.
Em notação matemática, a fórmula recorrente desse algoritmo escreve-se assim:
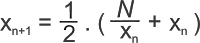
Vamos descrevê-lo passo a passo, supondo N = 2, isto é, estamos procurando o valor de ?2, que sabemos que é 1,414 213 562 373...
(1) "Joga-se" um valor qualquer, x0 > 0, para iniciar o processo. Esse valor é denominado semente. Vamos supor x0 = 1.
Evidentemente, 1 × 1 não é igual a 2.
Assim: x1 = 1/2 . (2/x0 + x0) => x1 = 1/2 . (2/1 + 1) = 1,5.
Mas 1,5 x 1,5 ? 2.
Então repete-se o algoritmo, agora com x1 = 1,5, para obtermos x2. Veja:
(2) x2 = 1/2 . (2/x1 + x1) => x2 = 1/2 . (2/1,5 + 1,5) = 1,41666... .
Já temos uma precisão até centésimos! Mais uma vez, para aumentar a precisão.
(3) Repete-se o algoritmo, agora com x2 = 1,41666..., para obtermos x3. Veja:
x3 = 1/2 . (2/x2 + x2) => x2 = 1/2 . (2/1,41666 + 1,41666) = 1,41421569...
A precisão já chegou à quinta casa decimal!
Só mais uma vez, tá? Prometo!
(4) x4 = 1/2 . (2/1,41421569 + 1,41421569) = 1,41421357...
Só mais um exemplo, com N = 16, para acreditarmos no "poder" desse algoritmo!
(1) Vamos supor x0 = 3,2; claro que 3,2 x 3,2 não dá 16. Então, vamos lá:
x1 = 1/2 . (16/x0 + x0) => x1 = 1/2 . (16/3,2 + 3,2) = 4,1(!)
Já está bem perto, não?
Vamos iterar para melhorar!
(2) x2 = 1/2 . (16/x1 + x1) => x2 = 1/2 . (16/4,1 + 4,1) = 4,00121951...(!)
Só mais uma "iteradazinha"!
(3) x3 = 1/2 . (16/x2 + x2) => x2 = 1/2 . (16/4,00121951 + 4,00121951) = 4,00000019...!
E aí,... dá para confiar no processo? Legal, não é?
Sugestões para treinar:
(1) ?3, com x0 = 1,5;
(2) ??, com x0 = 2;
(3) ?10, com x0 = 3;
(4) ?1000, com x0 = 30.
Existem processos semelhantes para se obter raízes cúbicas, quartas, etc. Só por curiosidade apresento abaixo a fórmula recorrente do algoritmo para a raiz cúbica:
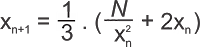
Tchau, abraço!
Prof. Carlos Torres.
No dicionário, iterar significa repetir. Um Processo Iterativo é a aplicação repetida de um mesmo algoritmo, até obter- se um resultado com a precisão desejada.
O algoritmo que vamos mostrar a seguir é um método simples de chegarmos à raiz quadrada de um número N, com excelente precisão, em três ou quatro iterações. Esse método já era usado na antiga Babilônia (2000 a.C.) e, posteriormente por Heron em Alexandria (10 d.C ? 70 d.C.).
Obviamente, é muito mais fácil pressionarmos as teclas "2" e "?" de uma calculadora para obtermos a raiz quadrada de dois. Mas,... e se a nossa calculadora não tiver a tecla "?", como podemos nos arranjar...? O algoritmo que vamos descrever era usado num tempo em que a ciência estava sendo escrita à luz de velas, em lápides de argila ou em folhas de papiro. É uma verdadeira "jóia" produzida pela inteligência humana!
Esse algoritmo é empregado ainda hoje (!) pelas calculadoras eletrônicas dotadas da tecla "?". Elas fazem os mesmos procedimentos que vamos fazer, só que num tempo muuuito menor.
Acompanhe. É interessante.
Em notação matemática, a fórmula recorrente desse algoritmo escreve-se assim:
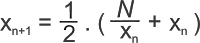
Vamos descrevê-lo passo a passo, supondo N = 2, isto é, estamos procurando o valor de ?2, que sabemos que é 1,414 213 562 373...
(1) "Joga-se" um valor qualquer, x0 > 0, para iniciar o processo. Esse valor é denominado semente. Vamos supor x0 = 1.
Evidentemente, 1 × 1 não é igual a 2.
Assim: x1 = 1/2 . (2/x0 + x0) => x1 = 1/2 . (2/1 + 1) = 1,5.
Mas 1,5 x 1,5 ? 2.
Então repete-se o algoritmo, agora com x1 = 1,5, para obtermos x2. Veja:
(2) x2 = 1/2 . (2/x1 + x1) => x2 = 1/2 . (2/1,5 + 1,5) = 1,41666... .
Já temos uma precisão até centésimos! Mais uma vez, para aumentar a precisão.
(3) Repete-se o algoritmo, agora com x2 = 1,41666..., para obtermos x3. Veja:
x3 = 1/2 . (2/x2 + x2) => x2 = 1/2 . (2/1,41666 + 1,41666) = 1,41421569...
A precisão já chegou à quinta casa decimal!
Só mais uma vez, tá? Prometo!
(4) x4 = 1/2 . (2/1,41421569 + 1,41421569) = 1,41421357...
Bom, aqui já temos o valor de ?2 com uma precisão até a sétima casa decimal, isto é, 1 parte em 10.000.000! Um erro de 2,1·10-7 %! Acho que está bom demais, não está? Então, até a sétima casa decimal, podemos dizer que ?2 = 1,4142135.
Só mais um exemplo, com N = 16, para acreditarmos no "poder" desse algoritmo!
(1) Vamos supor x0 = 3,2; claro que 3,2 x 3,2 não dá 16. Então, vamos lá:
x1 = 1/2 . (16/x0 + x0) => x1 = 1/2 . (16/3,2 + 3,2) = 4,1(!)
Já está bem perto, não?
Vamos iterar para melhorar!
(2) x2 = 1/2 . (16/x1 + x1) => x2 = 1/2 . (16/4,1 + 4,1) = 4,00121951...(!)
Só mais uma "iteradazinha"!
(3) x3 = 1/2 . (16/x2 + x2) => x2 = 1/2 . (16/4,00121951 + 4,00121951) = 4,00000019...!
E aí,... dá para confiar no processo? Legal, não é?
Sugestões para treinar:
(1) ?3, com x0 = 1,5;
(2) ??, com x0 = 2;
(3) ?10, com x0 = 3;
(4) ?1000, com x0 = 30.
Existem processos semelhantes para se obter raízes cúbicas, quartas, etc. Só por curiosidade apresento abaixo a fórmula recorrente do algoritmo para a raiz cúbica:
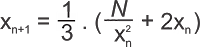
Tchau, abraço!
Prof. Carlos Torres.
loading...
- Leituras Do Blog
Crivo de Eratóstenes Borges e Nicolau Uma contribuição importante do matemático e filósofo gergo Eratóstenes (276 aC - 194 aC), foi o método usado para a determinação de todos o números primos, até um certo limite desejado, conhecido como Crivo...
- Leituras Do Blog
e, o número da natureza! Professor Carlos Magno Torres Em uma leitura anterior conhecemos algumas propriedades e particularidades muito interessantes do incrível número PI (?). Nesta leitura vamos conhecer outro magnífico número, conhecido...
- Leituras Do Blog
O Fantástico e Onipresente Número PI (?) Professor Carlos Magno Torres Pelo fato de o número pi ser representado por uma letra do alfabeto grego, poderíamos pensar que os antigos gregos tenham sido os primeiros a utilizá-lo....
- Leituras Do Blog
Eratóstenes Borges e Nicolau Eratóstenes, matemático e filósofo grego nasceu em 276 aC em Cirene, cidade da qual só restam ruinas, na atual Líbia, e morreu em 194 aC, na cidade de Alexandria. Foi diretor da Biblioteca de Alexandria, sendo...
- A Aceleração De Um Ponto Material é Definida Por A= -k/x. Determinou-se Exeperimentalmente Que V= 3m/s Quando X = 500mm. Obter A Velocidade Quando X = 750 Mm E A Posição Do Ponto Para A Qual Sua Velocidade é Nula.
Anônimo disse... no MUV, a aceleração é constante e x = at²/2, desse modo: x = at²/2 x = -kt² / 2x x² = -kt²/2 x = t.raiz.quadrada(-k/2), (com k =< 0) , lembrando que v = dx/dt, temos v = raiz.quadrada(-k/2) , para x = 500 mm, v = 3, então:...
