Física
Corrida Orbital
Professor Carlos Magno Torres
Seria possível vencer uma corrida diminuindo (!?) a velocidade de um veículo, isto é, freando em vez de acelerar? Parece meio sem sentido mas, com naves em órbita, é o único recurso! É uma mistura de habilidade e conhecimento da terceira lei de Kepler. Para melhor entender, acompanhe a análise da situação a seguir.
Rubens (R) e Miguel (M) estão em naves espaciais idênticas, gravitando em torno da Terra, numa mesma órbita circular de raio R0, com Miguel um pouco à frente de Rubens. Nessa situação ambos executam movimentos circulares uniformes de mesmo período T0, e mesma velocidade escalar orbital v0. Parece que não há como Rubens ultrapassar Miguel! Rubens, entretanto, conhecedor das leis de Kepler, engendra uma hábil e inteligente manobra.
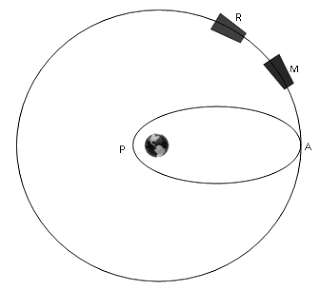
Ao se aproximar do ponto A da figura, Rubens aciona os retrofoguetes de sua nave, durante um intervalo de tempo suficiente para provocar uma pequena redução na sua velocidade orbital. Assim, sua nave passa a executar a órbita elíptica mostra-da, tendo a Terra como um dos focos dessa nova trajetória, o ponto A como apogeu e o ponto P como perigeu. Miguel, sem entender o que se passa, mantém seu movimento original.
Você deve estar se perguntando: Sim, ... mas onde está a esperteza de Rubens? Vamos ver.
De acordo com a terceira lei de Kepler, na órbita circular temos para ambas as naves período T0 e raio R0.
Entretanto, quando a nave de Rubens assume a órbita elíptica, o raio médio (a) dessa órbita passa a ser a metade do segmento AP e, portanto, menor que R0. Isso implica um novo período T para o movimento de Rubens, como podemos calcular pela terceira lei de Kepler:
T2/a3 = T02/R03 => T = (?(a3/R03).T0
Sendo a menor que R0, o novo período T também será menor que T0, e Rubens passará novamente pelo ponto A antes de Miguel, assumindo assim a dianteira!
Entretanto, para manter essa vantagem, ao se aproximar novamente do ponto A, Rubens deverá acelerar sua nave o suficiente para que ela volte a ter a mesma velocidade v0 do início, e continuar à frente de Miguel na órbita circular original.
Muito esperto esse Rubinho, não?!
Então é isso, estando em órbita, "desacelera que passa!" Surpresas da gravidade!
Atenção: Essa perigosa manobra requer muita habilidade. Não tente realizá-la sem uma orientação (da NASA, talvez)! Eh, eh, eh, ...
- Cursos Do Blog - Mecânica
Gravitação x Borges e Nicolau Johannes Kepler Johannes Kepler (1571-1630), notável astrônomo e matemático alemão, estabeleceu a forma como os planetas se movem em torno do Sol. Oito são os planetas de nosso sistema solar, na seguinte ordem de distância...
- Caiu No Vestibular
Vindos do espaço sideral (FUVEST) Alienígenas desejam observar o nosso planeta. Para tanto, enviam à Terra uma nave N, inicialmente ligada a uma nave auxiliar A, ambas de mesma massa. Quando o conjunto de naves se encontra muito distante da Terra,...
- Leituras Do Blog
A "Lei do inverso do quadrado da distância" ou "Lei da atração das massas" Professor Carlos Magno TorresVimos na leitura anterior a dedução de Newton para a aceleração da Lua relativa à Terra. A aceleração centrípeta. A partir dessa expressão,...
- Exercícios Resolvidos: Gravitação + Leis De Kepler 2
1. Considere um corpo A de massa 20kg. Para que este corpo atraia o planeta Terra com uma força de 50N, sua distância à superfície terrestre deve ser aproximadamente igual: a) ao raio da Terra; b) ao dobro do raio da Terra; c) ao quádruplo do raio...
- Exercícios Resolvidos Leis De Kepler. 2
(Direito. C.L.-97) Tendo em vista as Leis de Kepler sobre os movimento dos planetas, pode-se afirmar que: a) a velocidade de um planeta, em sua órbita, aumenta à medida que ele se afasta do sol. b) o período de revolução de um planeta é tanto maior...
Física
Ultrapassando na curva...
Corrida Orbital
Professor Carlos Magno Torres
Seria possível vencer uma corrida diminuindo (!?) a velocidade de um veículo, isto é, freando em vez de acelerar? Parece meio sem sentido mas, com naves em órbita, é o único recurso! É uma mistura de habilidade e conhecimento da terceira lei de Kepler. Para melhor entender, acompanhe a análise da situação a seguir.
Rubens (R) e Miguel (M) estão em naves espaciais idênticas, gravitando em torno da Terra, numa mesma órbita circular de raio R0, com Miguel um pouco à frente de Rubens. Nessa situação ambos executam movimentos circulares uniformes de mesmo período T0, e mesma velocidade escalar orbital v0. Parece que não há como Rubens ultrapassar Miguel! Rubens, entretanto, conhecedor das leis de Kepler, engendra uma hábil e inteligente manobra.

Ao se aproximar do ponto A da figura, Rubens aciona os retrofoguetes de sua nave, durante um intervalo de tempo suficiente para provocar uma pequena redução na sua velocidade orbital. Assim, sua nave passa a executar a órbita elíptica mostra-da, tendo a Terra como um dos focos dessa nova trajetória, o ponto A como apogeu e o ponto P como perigeu. Miguel, sem entender o que se passa, mantém seu movimento original.
Você deve estar se perguntando: Sim, ... mas onde está a esperteza de Rubens? Vamos ver.
De acordo com a terceira lei de Kepler, na órbita circular temos para ambas as naves período T0 e raio R0.
Entretanto, quando a nave de Rubens assume a órbita elíptica, o raio médio (a) dessa órbita passa a ser a metade do segmento AP e, portanto, menor que R0. Isso implica um novo período T para o movimento de Rubens, como podemos calcular pela terceira lei de Kepler:
T2/a3 = T02/R03 => T = (?(a3/R03).T0
Sendo a menor que R0, o novo período T também será menor que T0, e Rubens passará novamente pelo ponto A antes de Miguel, assumindo assim a dianteira!
Entretanto, para manter essa vantagem, ao se aproximar novamente do ponto A, Rubens deverá acelerar sua nave o suficiente para que ela volte a ter a mesma velocidade v0 do início, e continuar à frente de Miguel na órbita circular original.
Muito esperto esse Rubinho, não?!
Então é isso, estando em órbita, "desacelera que passa!" Surpresas da gravidade!
Atenção: Essa perigosa manobra requer muita habilidade. Não tente realizá-la sem uma orientação (da NASA, talvez)! Eh, eh, eh, ...
loading...
- Cursos Do Blog - Mecânica
Gravitação x Borges e Nicolau Johannes Kepler Johannes Kepler (1571-1630), notável astrônomo e matemático alemão, estabeleceu a forma como os planetas se movem em torno do Sol. Oito são os planetas de nosso sistema solar, na seguinte ordem de distância...
- Caiu No Vestibular
Vindos do espaço sideral (FUVEST) Alienígenas desejam observar o nosso planeta. Para tanto, enviam à Terra uma nave N, inicialmente ligada a uma nave auxiliar A, ambas de mesma massa. Quando o conjunto de naves se encontra muito distante da Terra,...
- Leituras Do Blog
A "Lei do inverso do quadrado da distância" ou "Lei da atração das massas" Professor Carlos Magno TorresVimos na leitura anterior a dedução de Newton para a aceleração da Lua relativa à Terra. A aceleração centrípeta. A partir dessa expressão,...
- Exercícios Resolvidos: Gravitação + Leis De Kepler 2
1. Considere um corpo A de massa 20kg. Para que este corpo atraia o planeta Terra com uma força de 50N, sua distância à superfície terrestre deve ser aproximadamente igual: a) ao raio da Terra; b) ao dobro do raio da Terra; c) ao quádruplo do raio...
- Exercícios Resolvidos Leis De Kepler. 2
(Direito. C.L.-97) Tendo em vista as Leis de Kepler sobre os movimento dos planetas, pode-se afirmar que: a) a velocidade de um planeta, em sua órbita, aumenta à medida que ele se afasta do sol. b) o período de revolução de um planeta é tanto maior...
